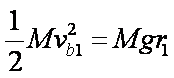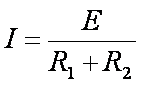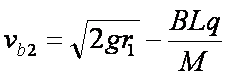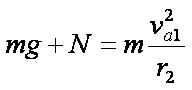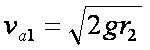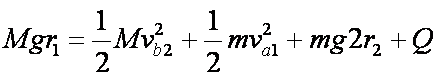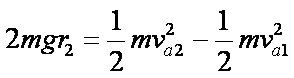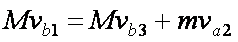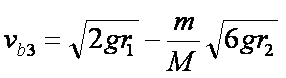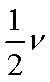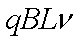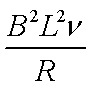- 电磁感应中的能量转化
- 共184题
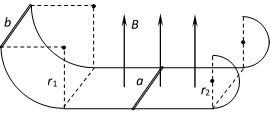
如图所示,宽度为L的平行光滑的金属轨道,左端为半径为r1的四分之一圆弧轨道,右端为半径为r2的半圆轨道,中部为与它们相切的水平轨道。水平轨道所在的区域有磁感应强度为B的竖直向上的匀强磁场。一根质量为m的金属杆a置于水平轨道上,另一根质量为M的金属杆b由静止开始自左端轨道最高点滑下,当b滑入水平轨道某位置时,a就滑上了右端半圆轨道最高点(b始终运动且a、b未相撞),并且a在最高点对轨道的压力大小为mg,此过程中通过a的电荷量为q,a、b棒的电阻分别为R1、R2,其余部分电阻不计。在b由静止释放到a运动到右端半圆轨道最高点过程中,
(1)在水平轨道上运动时b的最大加速度是多大?
(2)自b释放到a到达右端半圆轨道最高点过程中系统产生的焦耳热是多少?
(3)a刚到达右端半圆轨道最低点时b的速度是多大?
正确答案
见解析。
解析
(1)由机械能守恒定律:
∴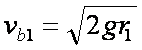
b刚滑到水平轨道时加速度最大,E=BLvb1
F安=BIL=Ma
∴ 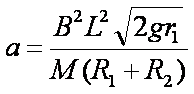
(2)∵ -BILt=Mvb2 –Mvb1 即 -BLq=M vb2 –Mvb1
∴
根据牛顿第三定律得:N=N΄=mg
∴
∵
∴
(3)∵
∴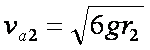
∵
∴
知识点
如图,光滑斜面的倾角为












正确答案
解析
略
知识点
如图,足够长的U型光滑金属导轨平面与水平面成
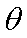
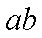
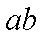


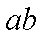
正确答案
解析
略。
知识点
如图所示,MN、PQ是足够长的光滑平行导轨,其间距为L,且MP⊥MN。导轨平面与水平面间的夹角θ=30° 。MP接有电阻R。有一匀强磁场垂直于导轨平面,磁感应强度为B0。将一根质量为m的金属棒ab紧靠MP放在导轨上,且与导轨接触良好,金属棒的电阻也为R,其余电阻均不计。现用与导轨平行的恒力F=mg沿导轨平面向上拉金属棒,使金属棒从静止开始沿导轨向上运动,金属棒运动过程中始终与MP平行。当金属棒滑行至cd处时已经达到稳定速度,cd 到MP的距离为s。
求:
(1)金属棒达到稳定速度的大小;
(2)金属棒从静止开始运动到cd的过程中,电阻R上产生的热量;
(3)若将金属棒滑行至cd处的时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,可使金属棒中不产生感应电流,写出磁感应强度B随时间t变化的关系式。
正确答案
见解析。
解析
(1)当金属棒稳定运动时,

解得: 
(2)由动能定理得:

∴
(3)当回路中的总磁通量不变时,金属棒中不产生感应电流。此时金属棒将沿导轨做匀加速运动。


知识点
如图所示,两电阻不计的足够长光滑平行金属导轨与水平面夹角






(1)乙金属杆刚进入磁场时,发现乙金属杆作匀速运动,则甲乙的电
(2)以刚释放时
(3)乙金属杆在磁场中运动时,乙金属杆中的电功率多少?
(4)若从开始释放到乙金属杆离开磁场,乙金属杆中共产生热量
正确答案
见解析
解析
(1)甲乙加速度相同(5m/s2),当乙进入磁场时,甲刚出磁场
乙进入磁场时
乙受力平衡 


(2)甲在磁场中运动时,
外力F始终等于安培力,
F方向沿导轨向下
(3)乙在磁场中作匀速运动,
(4)乙进入磁场前,甲乙发出相同热量,设为Q1,
此过程中甲一直在磁场中,外力F始终等于安培力,则有WF=W安=2 Q1 ⑥
乙在磁场中运动发出热量Q2,
利用动能定理mg
得Q2=0.02J ⑦
甲乙发出相同热量Q1=(Q-Q2)/2=1/75=0.0133J
由于甲出磁场以后,外力F为零。
得WF=2 Q1 =2/75=0.0266J
(另解:整个过程 甲、乙通过的电流相同,所以发出的热量相同,
总热量为2Q=0.0667J
根据能量守恒,由于甲在磁场中是a=5m/s =gsinθ,所以 甲金属杆下滑时 重力做功全部转化成动能,外力做功WF转化成电能。离开磁场后外力为零,不做功。
乙金属杆进入磁场后,是匀速运动,重力做功转化为电能,WG=mglsinθ=0.04J
WF + WG=2Q
WF =2Q- WG= 0.0267 (J)
知识点
扫码查看完整答案与解析