- 平行向量与共线向量
- 共69题
16.在△ABC中,角A,B,C的对边分别为a,b,c.设向量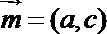
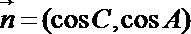
(1)若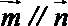
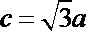
(2)若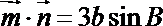
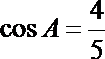
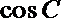
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.设向量


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.若A,B是锐角三角形

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点为





(Ⅰ)求
(Ⅱ)若



正确答案
解:
(1)

联立直线方程,化简为
设A(





当K不存在时,

综上,
(2)
由韦达定理知 

当
当



解析
解析已在路上飞奔,马上就到!
知识点
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2).
(1)若|c|=2
(2)若|b|=
正确答案
(1)令c=(x,y),则由|c|=2


又由a∥c知,2x-y=0②
联立①②可解得:

故c=(2,4)或c=(-2,-4).
(2)由a+2b与2a-b垂直知(a+2b)·(2a-b)=0,
即2a2+3a·b-2b2=0,∴a·b=
即|a||b|cosθ=

而由a=(1,2)知|a|=

∵θ∈[0,π],∴θ=π.
解析
解析已在路上飞奔,马上就到!
知识点
13. 已知



正确答案
解析
因为向量b与向量c平行,
所以s=(-1)*2=-2.
所以
所以答案为
考查方向
解题思路
先根据向量平行求解出s的值,进而求出余弦值
易错点
向量平行的计算
知识点
9. 已知抛物线C:


正确答案
解析
直线PF的方程为y=x-2,与抛物线方程联立,解得x=4,所以
考查方向
解题思路
本题考查抛物线的简单几何性质,解题步骤如下:1、由题可知,易得直线PF的方程。2、将直线方程与抛物线联立,解得
易错点
本题易在求解时把分母平方运算。
知识点
2.若平面向量a=(m,1),b=(2,1),且(a-2b)//b,则m =( )
正确答案
解析
因为a-2b =(m-4,-1), b=(2,1)且(a-2b)//b,所以m-4= -2, 则m=2.
考查方向
解题思路
把向量a-2b的坐标表示出来,根据两个向量平行公式,建立关于m的方程, 即可求出m的值。
易错点
向量的平行或垂直的公式容易弄混淆。
知识点
4.设


正确答案
解析



所以
考查方向
解题思路
由基本运算入手
易错点
考虑过多,想到向量的零向量,以及向量平行的同向和反向两种情况而误导出错
知识点
3. 若


正确答案
解析
因为
考查方向
解题思路
根据向量平行时数量积的特点进行求解
易错点
混淆向量平行和向量垂直时,向量数量积不同。
知识点
扫码查看完整答案与解析































