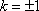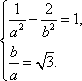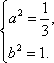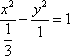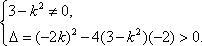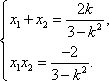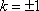- 双曲线的几何性质
- 共199题
22.如图已知椭圆






(1)求椭圆
(2)已知垂直于








(3)在






正确答案
(1)由题设得
解得: 
故

(2)证明:

直线

①×②,得

代入③得

因为点


即点

(3)设直线
结合第(2)问的结论

所以
解析
解析已在路上飞奔,马上就到!
知识点
双曲线
正确答案
解析
知识点
在平面直角坐标系下,曲线



正确答案


解析
化为普通方程后,圆心到直线的距离小于或等于圆的半径(
知识点
抛物线

正确答案
解析
略
知识点
已知点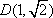
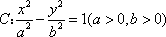
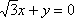
(1)求双曲线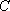
(2)若过点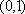
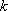
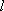
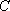
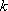
(3)设(2)中直线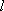
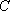
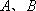
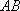
正确答案
(1)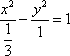
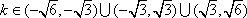
解析
(1)由题知,有
解得
因此,所求双曲线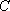
(2) ∵直线
∴直线
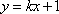
联立方程组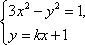
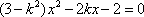
又直线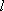
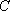
∴
解得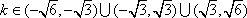
(3)设交点为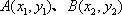
又以线段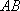
因此,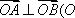
于是,
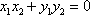
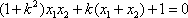
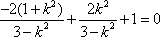
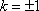
又
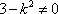
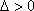
所以,所求实数
知识点
直线


正确答案
解析
略
知识点
设




正确答案
解析
:设点P的横坐标为x0,
∵y=x2+2x+3,
∴y'
利用导数的几何意义得2x0+2=tanα(α为点P处切线的倾斜角),
又∵
∴
知识点
已知双曲线
正确答案
解析
略
知识点
如图所示,在四棱锥P-ABCD中,底面ABCD是边长为a的正方形,侧面

(1)求证:EF//平面PAD;
(2)求三棱锥F-DEC的体积;
(3)在线段CD上是否存在一点G,使得平面
正确答案
见解析。
解析
知识点
设点P是双曲线




正确答案
解析
略。
知识点
扫码查看完整答案与解析