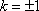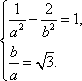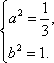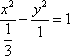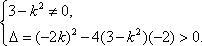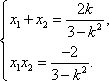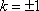- 双曲线的几何性质
- 共199题
1
题型:简答题
|
22.如图已知椭圆






(1)求椭圆
(2)已知垂直于








(3)在






正确答案
(1)由题设得
解得: 
故

(2)证明:

直线

①×②,得

代入③得

因为点


即点

(3)设直线
结合第(2)问的结论

所以
解析
解析已在路上飞奔,马上就到!
知识点
椭圆的定义及标准方程双曲线的几何性质
1
题型:填空题
|
双曲线
正确答案
解析
知识点
双曲线的几何性质
1
题型:填空题
|
抛物线

正确答案
解析
略
知识点
点到直线的距离公式双曲线的几何性质抛物线的标准方程和几何性质
1
题型:简答题
|
已知点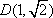
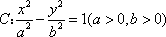
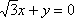
(1)求双曲线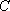
(2)若过点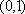
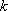
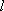
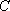
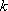
(3)设(2)中直线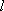
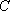
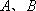
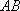
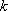
正确答案
(1)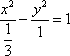
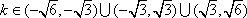
解析
(1)由题知,有
解得
因此,所求双曲线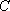
(2) ∵直线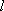
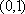
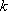
∴直线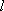
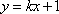
联立方程组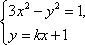
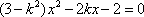
又直线
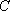
∴
解得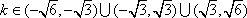
(3)设交点为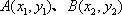
又以线段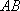
因此,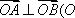
于是,
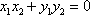
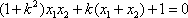
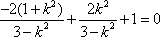
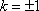
又
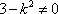
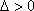
所以,所求实数
知识点
双曲线的几何性质
1
题型:
单选题
|
已知双曲线
正确答案
D
解析
略
知识点
双曲线的几何性质
下一知识点 : 双曲线的相关应用
扫码查看完整答案与解析