- 双曲线的几何性质
- 共199题
由曲线y=x2,y=x3围成的封闭图形面积为 。
正确答案
解析
要求曲线y=x2,y=x3围成的封闭图形面积,根据定积分的几何意义,只要求∫01(x2﹣x3)dx即可。
解:由题意得:所求封闭图形的面积为
∫01(x2﹣x3)dx═(

=
故答案为:
知识点
若抛物线y2=2px(p>0)的焦点与双曲线
正确答案
8
解析
双曲线
∴双曲线
∵抛物线y2=2px(p>0)的焦点与双曲线
∴
∴p=8
故答案为:8
知识点
设





正确答案
解析
由


知识点
已知双曲线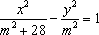
正确答案
解析
略
知识点
设双曲线

正确答案
解析
略
知识点
以双曲线
正确答案
解析
易知椭圆中
知识点
已知点








(1)求双曲线
(2)若双曲线


(3)过圆






正确答案
见解析
解析
(1)设


因为点




在



由双曲线的定义可知:
故双曲线

(2)由条件可知:两条渐近线分别为
设双曲线

则点

所以

因为



故
(3)解一:因为


所以切线


代入双曲线
两边除以


设

由韦达定理知:

所以

解二:设


①当


所以:
又
所以
②当
所以
知识点
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是
(1)求双曲线方程
(2)动直线



正确答案
见解析
解析
(1)如图,设双曲线方程为

由已知得
解得
所以所求双曲线方程为

(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)………………………8分
假设存在直线
设M(x1,y1),N(x2,y2)


∴l的方程为y=
由
∵Δ=16-4×28<0,∴所求直线

知识点
已知函数
(1)求
(2)若将


正确答案
见解析。
解析
(1)
=
所以

(2)∵将


∴
∵
∴当
当
知识点
若圆锥的内切球与外接球的球心重合,且内切球的半径为
正确答案
解析
过圆锥的旋转轴作轴截面,得△











知识点
扫码查看完整答案与解析























