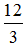一元高次不等式的解法
共47题

一元高次不等式的解法
共47题

热门试卷

题型：简答题

简答题 · 12 分

某种家电器每台的销售利润与该电器无故障使用时间T（单位：年）有关，若T≤1，则销售利润为0元，若1＜T≤3，则销售利润为100元，若T＞3，则销售利润为200元，设每台该种电台无故障使用时间T≤1，1＜T≤3及T＞3这三种情况发生的概率为P1，P2，P3，又知P1，P2是方程25x2﹣15x+a=0的两个根，且P2=P3，

（1）求P1，P2，P3的值；

（2）记ξ表示销售两台这种家用电器的销售利润总和，求ξ的分布列和期望

正确答案

见解析

解析

（1）由已知P1+P2+P3=1，

∵ P2=P3，∴P1+2P2=1

∵ P1，P2是方程25x2﹣15x+a=0的两个根，

∴

（2）ξ的可能取值为0，100，200，300，400

∴ 随机变量ξ的分布列为：

元

知识点

一元高次不等式的解法

题型：填空题

填空题 · 5 分

已知点为抛物线的焦点，为原点，点是抛物线准线上一动点，在抛物线上，且＝4，则＋的最小值是______.

正确答案

解析

如图，可求,再求关于抛物线的准线的对称点，因此，当三点共线时取到最小值，即

知识点

一元高次不等式的解法

题型：单选题

单选题 · 5 分

一个几何体的三视图如图所示，则该几何体的体积为

A12

B11

正确答案

解析

由三视图可知原几何体是高为3，底面是矩形的四棱锥，其中底面矩形的长和宽分别是4和3，所以该几何体的体积是 ×3×4×3=12.故选A.

知识点

一元高次不等式的解法

题型：填空题

填空题 · 5 分

设若存在实数，使得函数有两个零点，则的取值范围是 .

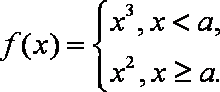
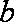
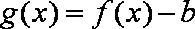
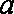
正确答案

答案：

解析

略

知识点

一元高次不等式的解法

题型：填空题

填空题 · 5 分

在约束条件下,过点的线性目标函数取得最大值10,则线性目标函数___ （写出一个适合题意的目标函数即可）；

正确答案

答案：z=x+9y

解析

根据已知线性约束条件可知，不等式组表示的平面区域为下图所示，

线性目标函数，那么过点（1,1）取得最大值为10，因此只要满足且；因此可以为。

知识点

一元高次不等式的解法

继续学习学习下一知识点

下一知识点 : 其它不等式的解法

百度题库 > 高考 > 理科数学 > 一元高次不等式的解法

扫码查看完整答案与解析