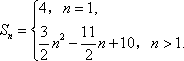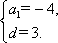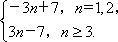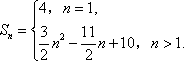- 等比数列的性质及应用
- 共160题
已知等差数列{an}前三项的和为-3,前三项的积为8.
(1)求等差数列{an}的通项公式;
(2)若a2,a3,a1成等比数列,求数列{|an|}的前n项和。
正确答案
(1) an=-3n+5或an=3n-7 ;(2)
解析
(1)设等差数列{|an|}的公差为d,则a2=a1+d,a3=a1+2d,
由题意得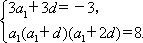
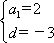
所以由等差数列通项公式可得
an=2-3(n-1)=-3n+5或an=-4+3(n-1)=3n-7.
故an=-3n+5或an=3n-7.
(2)当an=-3n+5时,a2,a3,a1分别为-1,-4,2,不成等比数列,不满足条件;
当an=3n-7时,a2,a3,a1分别为-1,2,-4,成等比数列,满足条件。
故|an|=|3n-7|=
记数列{|an|}的前n项和为Sn.
当n=1时,S1=|a1|=4;
当n=2时,S2=|a1|+|a2|=5;
当n≥3时,
Sn=S2+|a3|+|a4|+…+|an|=5+(3×3-7)+(3×4-7)+…+(3n-7)
=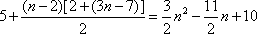
当n=2时,满足此式。
综上,
知识点
设


正确答案
解析
通过



知识点
已知数列{an}的前n项和为Sn,且Sn=2n2+n,n∈N*,数列{bn}满足an=4log2bn+3,n∈N*。
(1)求an,bn;
(2)求数列{an·bn}的前n项和Tn。
正确答案
(1)an=4n-1,n∈N*, bn=2n-1,n∈N*(2)Tn=(4n-5)2n+5,n∈N*
解析
(1)由Sn=2n2+n,得当n=1时,a1=S1=3;
当n≥2时,an=Sn-Sn-1=4n-1。
所以an=4n-1,n∈N*。
由4n-1=an=4log2bn+3,得bn=2n-1,n∈N*。
(2)由(1)知anbn=(4n-1)·2n-1,n∈N*。
所以Tn=3+7×2+11×22+…+(4n-1)·2n-1,2Tn=3×2+7×22+…+(4n-5)·2n-1+(4n-1)·2n,
所以2Tn-Tn=(4n-1)2n-[3+4(2+22+…+2n-1)]=(4n-5)2n+5。
故Tn=(4n-5)2n+5,n∈N*
知识点
若等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=__________;前n项和Sn=__________.
正确答案
2;2n+1-2
解析
根据等比数列的性质知a3+a5=q(a2+a4),
∴q=2,又a2+a4=a1q+a1q3,故求得a1=2,
∴Sn=
知识点
设首项为1,公比为
正确答案
解析

知识点
扫码查看完整答案与解析