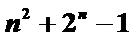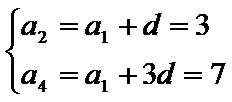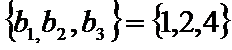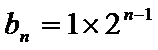- 等比数列的性质及应用
- 共160题
8.已知{an}是等差数列,Sn是其前n项和.若a1+a22=
正确答案
20
知识点
15.设数列



正确答案
15
解析
数列



+2+4+8=15.
考查方向
解题思路
分别计算出每一项,再相加即可。
易错点
弄错符号。
知识点
3.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还。”其意思为:“有
正确答案
解析
由题意可知

考查方向
解题思路
由已知可得等比数列的公比是1/2,前六项的和为378,可以求出首项,进一步求出第二项即可。
易错点
不会转化为等比数列来做。
知识点
10.设





正确答案
解析
设等比数列


考查方向
解题思路
利用等比数列的性质,将
易错点
1、等比数列求和的性质不能正确使用,注意的是“片段和”,而不是“和”。
2、本题不容易联系到基本不等式,并正确地使用不等式:一正二定三相等。
知识点
14.各项均为正数的等比数列



正确答案
解析
试题分析:由




考查方向
解题思路
直接利用等比数列的通项公式进行计算。
易错点
相关知识点不熟悉导致出错。
知识点
7. 已知等比数列



正确答案
解析
由


考查方向
解题思路
由

易错点
公比的正负情况不知道。
知识点
17.已知数列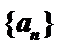
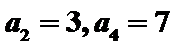
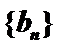
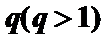
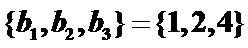
(Ⅰ)求数列

(Ⅱ)求数列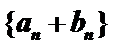
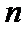
正确答案
(1)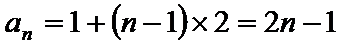
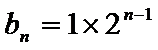
解析
试题分析:本题属于数列中的基本问题,题目的难度不大,(1)直接按照步骤来求(2)利用求和公式来解.
(Ⅰ)设等差数列的首项和公差分别为: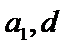
解得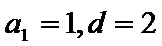

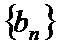
∴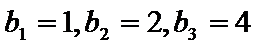
∴
(Ⅱ)
=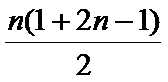
= 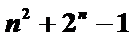
考查方向
解题思路
本题考查等差数列和等比数列以及数列的求和,解题步骤如下:
用待定系数法构造关于首项和公差公比的方程组。
等差等比的求和公式。
易错点
第2问不知道分组求和。
知识点
3.在等比数列


正确答案
解析
因为等比数列中,




考查方向
解题思路
根据等比数列的性质求出公比q的值,然后求出前五项的积
易错点
计算错误;概念理解错误
知识点
17.设数列




(1)求数列

(2)设



正确答案
(1)

(2)
解析
(1)



(2)
两式相减得
考查方向
本题主要考查了数列的通项公式和求和
解题思路
(1)利用
(2)利用错位相减法求出前n项和本题考查导数的性质,
易错点
(1)利用定义求通项公式
(2)第二问中错位相减法计算的准确性;
知识点
6.设


正确答案
解析
根据题意知,


考查方向
本题主要考查了等比数列与均值不等式的综合应用,在近几年的各省高考题出现的频率较高,常与数列、不等式等知识点交汇命题。
易错点
均值不等式取等条件容易忽视。
知识点
扫码查看完整答案与解析