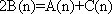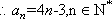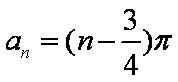- 等比数列的性质及应用
- 共160题
设




正确答案
解析
由
选B。
知识点
已知数列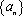
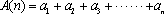
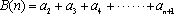
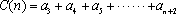
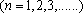
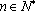
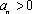
(1)若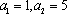
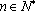
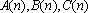
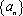
(2)证明:数列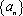
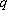
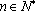
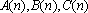
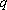
正确答案
见解析
解析
解析:(1)
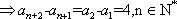
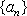
(2)(必
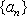
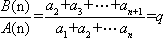
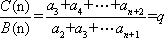
(充分性):若对于任意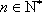
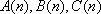
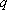
则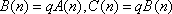
于是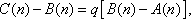
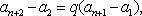
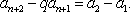
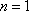
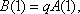
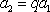
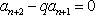
因为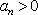
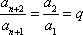

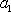
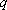
综上,数列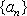
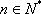

知识点
在数列









(1)求证:
(2)设


正确答案
见解析。
解析
(1)由



由



①

所以

(2)由(1)知,
①

③

代入

所以
整理得,
所以
由

所以

当



当



故使



知识点
各项为正数的数列





(1)求

(2)求数列
(3)是否存在正整数



正确答案
见解析。
解析
知识点
数列






(1)求
(2)求
正确答案
见解析。
解析
(1)


∵



解得

当


(2)当



得
又


当
知识点
已知数列










正确答案
解析
略
知识点
函数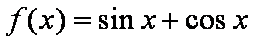

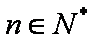
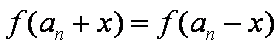
正确答案
解析
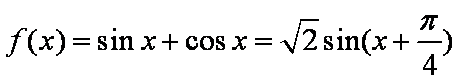
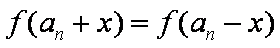
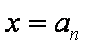
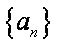
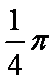
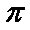
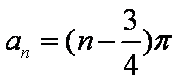
知识点
已知数列





(1)求证:数列

(2)设数列











正确答案
见解析。
解析
(1)因为

则
所以
又




即

(2)由(1)知

①当



若




因为




所以(
②当



则

即

欲满足题设条件,只需

因为


即
综上所述,当


当


知识点
已知数列


(1)试求

(2)试求

(3)若






正确答案
见解析
解析
(1)由




(2)




要使


解得




(3)选取


由(2)的结论知


又


知识点
某高科技企业研制出一种型号为







(1)求数列

(2)记






正确答案
见解析
解析
(1)由题设,知




故









故


于是,

(2)由(1)知,

当



所以
当

当



所以,当


故该企业需要在第11年年初更换
知识点
扫码查看完整答案与解析