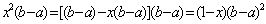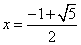- 等比数列的性质及应用
- 共160题
抛物线y2=4x的准线方程是 。
正确答案
x=﹣1
解析
∵2p=4，
∴p=2，开口向右，
∴准线方程是x=﹣1。
故答案为x=﹣1。
知识点
已知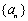
（1）当
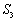
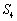
（2）当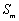
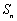
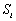
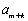
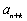
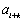
正确答案
见解析
解析
（1）由已知，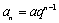
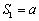
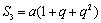
当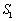
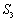
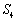
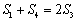
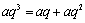
化简得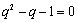
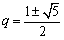
（2）若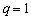
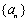
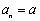
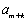
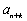
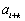
若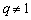
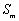
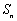
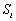
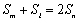
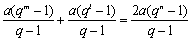
整理得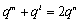
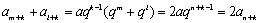
所以，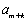
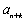
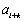
知识点
当x∈[﹣2，1]时，不等式ax3﹣x2+4x+3≥0恒成立，则实数a的取值范围是（ ）
A[﹣5，﹣3]
B[﹣6，﹣
C[﹣6，﹣2]
D[﹣4，﹣3]
正确答案
解析
当x=0时，不等式ax3﹣x2+4x+3≥0对任意a∈R恒成立；
当0＜x≤1时，ax3﹣x2+4x+3≥0可化为a≥
令f（x）=
当0＜x≤1时，f′（x）＞0，f（x）在（0，1]上单调递增，
f（x）max=f（1）=﹣6，∴a≥﹣6；
当﹣2≤x＜0时，ax3﹣x2+4x+3≥0可化为a≤
由（*）式可知，当﹣2≤x＜﹣1时，f′（x）＜0，f（x）单调递减，当﹣1＜x＜0时，f′（x）＞0，f（x）单调递增，
f（x）min=f（﹣1）=﹣2，∴a≤﹣2；
综上所述，实数a的取值范围是﹣6≤a≤﹣2，即实数a的取值范围是[﹣6，﹣2]。
知识点
设
正确答案
解析
若已知
知识点
商家通常依据“乐观系数准则”确定商品销售价格，及根据商品的最低销售限价a，最高销售限价b（b＞a）以及常数x（0＜x＜1）确定实际销售价格c=a+x（b-a），这里，x被称为乐观系数。
经验表明，最佳乐观系数x恰好使得（c-a）是（b-c）和（b-a）的等比中项，据此可得，最佳乐观系数x的值等于_____________。
正确答案
解析
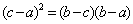
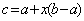
又b＞a可得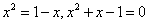
知识点
扫码查看完整答案与解析