- 不等式的实际应用
- 共11题
7.某公司为激励创新,计划逐年加大研发奖金投入。若该公司2015年全年投入研发奖金130万元,在此基础上,每年投入的研发奖金比上一年增长12%,则该公司全年投入的研发奖金开始超过200万元的年份是(参考数据:lg1.12=0.05,lg1.3=0.11,lg2=0.30) ( )
正确答案
解析
试题分析:设从2015年后第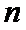
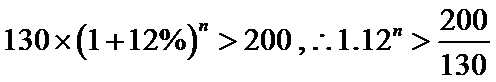
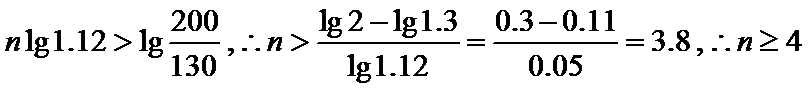
考查方向
解题思路
本题先根据题意得出不等式,然后两边同取对数,可以得到n的范围,求出奖金开始超过200万元的年份.
易错点
本题在解不等式的时候想不到两边取对数的技巧
知识点
16.命题p:“


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17. 已知△ABC是半径为R的圆内接三角形,且2R·(sin2A-sin2C)=(a-b)sin B.
(1)求角C;
(2)试求△ABC的面积S的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设数列




(Ⅰ)若

(Ⅱ)若

(Ⅲ)若

正确答案
(Ⅰ)由题意,得
解
得
∴
即
(Ⅱ)由题意,得
由

根据


当

∴

(Ⅲ)假设存在p和q满足条件,
由不等式


∵
根据
对于任意的正整数m 都有

即
当

得

当

得
解得
∴ 存在p和q,使得
p和q的取值范围分别是

解析
解析已在路上飞奔,马上就到!
知识点
9.不等式


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析




