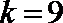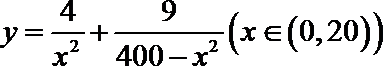- 基本不等式及不等式的应用
- 共164题
7.若实数


正确答案
解析




考查方向
解题思路
根据


易错点
不会利用基本不等式得到
知识点
21.两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧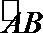
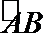
(1)将y表示成x的函数;
(2)判断弧
正确答案
(1)由题意得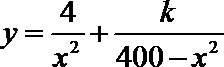
又∵当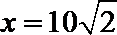
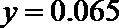
∴
∴
(2)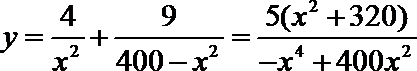
令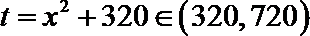
则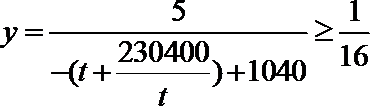
当且仅当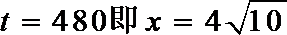
∴弧AB上存在一点,该点到城A的距离为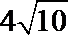
解析
解析已在路上飞奔,马上就到!
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
7.设


正确答案
解析
首先画出现行约束条件所标示的平面区域。然后将线性目标函数改写成斜截式,y=-3x+z。平移直线束,在y轴上截距最小时,将对应的x=0、y=1带入目标函数,得z=0+1=1。所以答案选B。
考查方向
本题考查线性规划知识,可行域的画法,及目标函数的最值的求解。
解题思路
首先必须画出现行约束条件所标示的平面区域。然后将线性目标函数改写成斜截式,y=-3x+z。平移直线束,在y轴上截距最小时,将对应的x、y带入即可。
易错点
将线性目标函数转换成直线束的时候,容易出错。注意y=-3x,而且z最小,则对应的目标函数y=-3x+z在y轴上的截距为最小。
教师点评
在解线性规划问题时,首先按照直线定域、特殊点定界的原则,正确画出平面区域;然后将目标函数写成斜截式,平移直线束,观察在y轴上的截距为最小或最大时对应的x、y的值,带入目标函数求解即可。
知识点
18.某房地产开发公司计划在一楼区内建造一个长方形公园





(1)若设休闲区的长和宽的比




(2)要使公园所占面积最小,休闲区
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
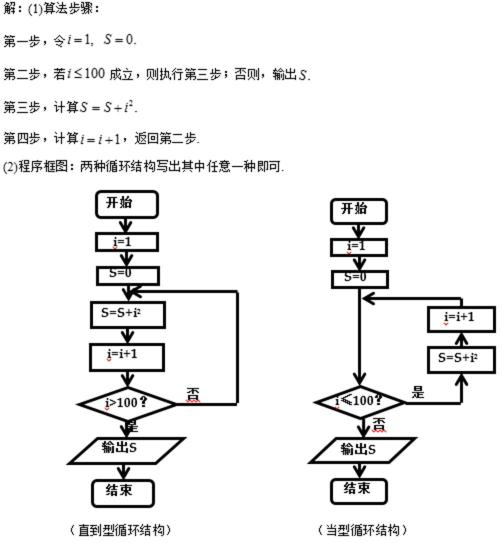
18. 设计一个算法求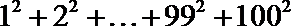
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.甲、乙两公司同时开发同一种新产品,经测算,对于函数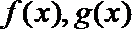
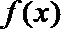
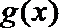
(1)试解释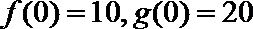
(2)设
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.某工厂去年某产品的年产量为100万只,每只产品的销售价为10元,固定成本为8元.今年,工厂第一次投入100万元(科技成本),并计划以后每年比上一年多投入100万元(科技成本),预计产量年递增10万只,第n次投入后,每只产品的固定成本为


(1)求k的值,并求出
(2)问从今年算起第几年利润最高?最高利润为多少万元?
正确答案
(1)由
所以
(2)由

当且仅当
解析
解析已在路上飞奔,马上就到!
知识点
14.己知平行四边形的周长为6,则其对角线长的平方和的最小值是 .
正确答案
9
解析
试题分析:本题属于平面向量和基本不等式的问题,题目的难度较小。注意转化为平面向量求解。
考查方向
本题主要考查了平面向量和基本不等式的问题。
解题思路
本题考查平面向量,解题步骤如下:
设平行四边形的两邻边分别为向量a,b,夹角为θ。则对角线的平方和为(a+b)2+(a-b)2=2a2+2b2≥(a+b)2=9。
易错点
本题必须注意转化为平面向量的问题求解,忽视则会出现错误。
知识点
20.小明同学制作了一个简易的网球发射器,可用于帮忙练习定点接发球,如图1所示,网球场前半区、后半区总长为23.77米,球网的中间部分高度为0.914米,发射器固定安










正确答案
(1)由




(Ⅱ)网球发过球网,满足
所以

因此

依题意:关于k的方程 

即

得

解析
本题是函数的应用,将实际问题与函数联系起来,有利于学生对函数的理解。
考查方向
函数的应用
解题思路
最大射程就是最大值,是网球落地的横坐标
易错点
实际问题和函数模型的转换
知识点
扫码查看完整答案与解析