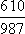- 循环结构
- 共36题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
执行如图所示的程序框图,输出的S值为( )。
正确答案
解析
依次执行的循环为S=1,i=0;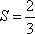
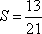
知识点
已知双曲线E:

(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1,l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由。
正确答案
(1)因为双曲线E的渐近线分别为l1:y=2x,l2:y=﹣2x,
所以
所以
故c=
从而双曲线E的离心率e=

(2)由(1)知,双曲线E的方程为

设直线l与x轴相交于点C,
当l⊥x轴时,若直线l与双曲线E有且只有一个公共点,则|OC|=a,|AB|=8,
所以
因此


以下证明:当直线l不与x轴垂直时,双曲线双曲线E的方程为

设直线l的方程为y=kx+m,依题意,得k>2或k<﹣2;
则C(﹣
由


由S△OAB=




因为4﹣k2<0,
所以△=4k2m2+4(4﹣k2)(m2+16)=﹣16(4k2﹣m2﹣16),
又因为m2=4(k2﹣4),
所以△=0,即直线l与双曲线E有且只有一个公共点。
因此,存在总与直线l有且只有一个公共点的双曲线E,且E的方程为

解析
压轴题;圆锥曲线的定义、性质与方程。
(1)依题意,可知

(2)由(1)知,双曲线E的方程为






知识点
设函数f(x)=ln x-ax,g(x)=ex-ax,其中a为实数。
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;
(2)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论。
正确答案
(1) a∈(e,+∞); (2) 当a≤0或a=e-1时,f(x)的零点个数为1,
当 0<a<e-1时,f(x)的零点个数为2.
解析
(1)令f′(x)=

综上,有a∈(e,+∞)。
(2)当a≤0时,g(x)必为单调增函数;当a>0时,令g′(x)=ex-a>0,解得a<ex,即x>ln a.
因为g(x)在(-1,+∞)上是单调增函数,类似(1)有ln a≤-1,即0<a≤e-1.
结合上述两种情况,有a≤e-1.
①当a=0时,由f(1)=0以及f′(x)=
②当a<0时,由于f(ea)=a-aea=a(1-ea)<0,f(1)=-a>0,且函数f(x)在[ea,1]上的图象不间断,所以f(x)在(ea,1)上存在零点。
另外,当x>0时,f′(x)=
③当0<a≤e-1时,令f′(x)=
当-ln a-1=0,即a=e-1时,f(x)有一个零点x=e.
当-ln a-1>0,即0<a<e-1时,f(x)有两个零点。
实际上,对于0<a<e-1,由于f(e-1)=-1-ae-1<0,f(a-1)>0,且函数f(x)在[e-1,a-1]上的图象不间断,所以f(x)在(e-1,a-1)上存在零点。
另外,当x∈(0,a-1)时,f′(x)=
下面考虑f(x)在(a-1,+∞)上的情况,先证f(ea-1)=a(a-2-ea-1)<0.
为此,我们要证明:当x>e时,ex>x2.设h(x)=ex-x2,则h′(x)=ex-2x,再设l(x)=h′(x)=ex-2x,则l′(x)=ex-2.
当x>1时,l′(x)=ex-2>e-2>0,所以l(x)=h′(x)在(1,+∞)上是单调增函数,故当x>2时,h′(x)=ex-2x>h′(2)=e2-4>0,
从而h(x)在(2,+∞)上是单调增函数,进而当x>e时,
h(x)=ex-x2>h(e)=ee-e2>0.即当x>e时,ex>x2.
当0<a<e-1,即a-1>e时,f(ea-1)=a-1-aea-1=a(a-2-ea-1)<0,又f(a-1)>0,且函数f(x)在[a-1,ea-1]上的图象不间断,所以f(x)在(a-1,ea-1)上存在零点,又当x>a-1时,f′(x)=
综合①,②,③,当a≤0或a=e-1时,f(x)的零点个数为1,
当 0<a<e-1时,f(x)的零点个数为2.
知识点
当

正确答案
解析
知识点
扫码查看完整答案与解析