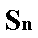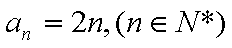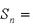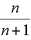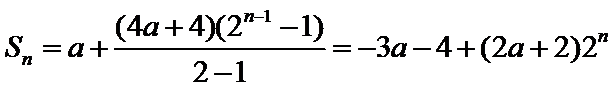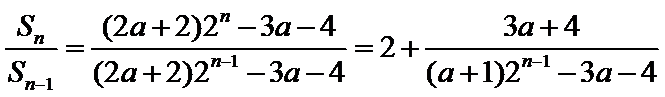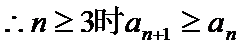- 函数的基本性质
- 共1471题
设函数f(x)=|x-1| +|x-a|,
(1)当a =4时,求不等式f(x) 
(2)若

正确答案
见解析
解析
解析:(1)



解得:

故不等式


(2)因为: 

所以: 
由题意得:



知识点
一个几何体的三视图如图所示,则该几何体的体积的是( )
正确答案
解析
略
知识点
已知数列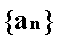
(1)求数列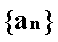
(2)设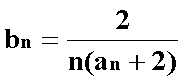
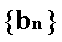
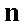
正确答案
(1)
(2)
解析
(1)设数列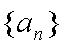
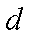
由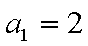
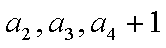
解得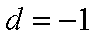
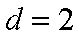
当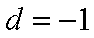
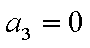
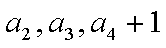
所以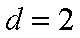
∴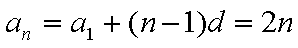
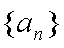
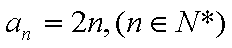
(2)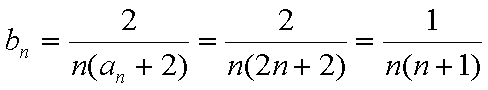
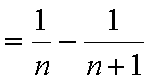
∴
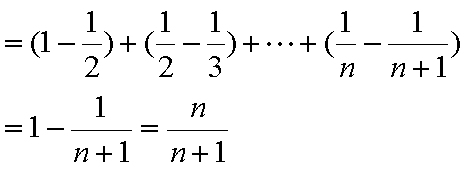
………………………12分
知识点
18.设命题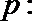
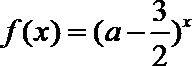
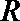
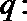
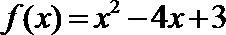
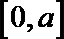
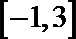
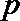
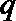
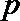
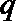
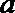
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
22.已知焦点在





(1)求椭圆
(2)已知过点




(3)若直线


正确答案
(1)设椭圆

且
由题意可知:

所以
所以,椭圆
(2)由(1)得
当直线


由
解得:

即


则直线
直线
因为
所以
所以
解析
解析已在路上飞奔,马上就到!
知识点
4.若函数

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.已知数列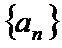
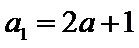
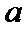
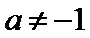
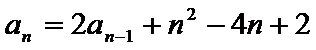
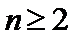
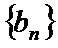
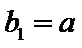
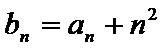
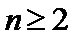
(1)证明: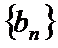
(2)设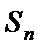
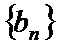
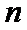
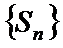
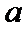
(3)当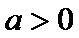
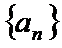
正确答案
(1)∵
∴
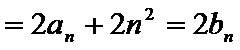
由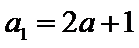
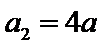
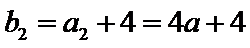
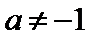
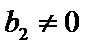
即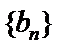
(2)
当n≥2时,
∵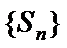
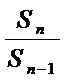
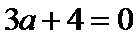
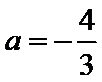
(3)由(1)知当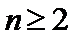
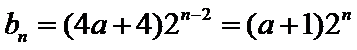
所以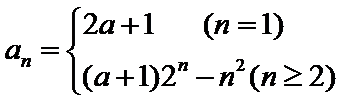
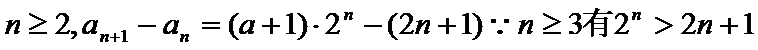
显然最小项是前三项中的一项.
当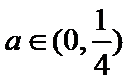
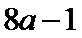
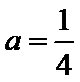
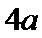
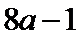
当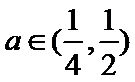
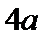
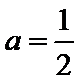
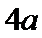
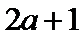
当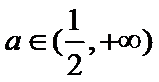
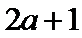
解析
解析已在路上飞奔,马上就到!
知识点
6.定义在





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.函数
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
5.下列函数中,既是偶函数,又在区间
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析