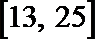- 函数的基本性质
- 共1471题
12.若函数

正确答案
知识点
14. 已知函数


正确答案
解析
试题分析:由函数




考查方向
解题思路
根据函数的单调性先求出

易错点
不知如何应用已知条件
知识点
7.已知函数


①

②当


③当

④
其中正确的是( )
正确答案
解析
由图像可知函数的值域为











考查方向
解题思路
先画出函数
易错点
不能准确画出函数的图像导致本题出错。
知识点
3.下列函数中,既是奇函数,又是在区间
正确答案
解析
A. 












考查方向
解题思路
先求定义域,判断奇偶性,再利用性质判断单调性
易错点
本题易在函数指数函数、对数函数、幂函数混淆
知识点
14.定义在某区间上的函数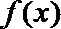
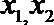
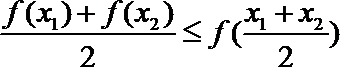
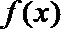
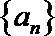
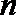
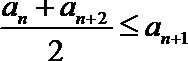
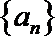
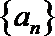
(1)数列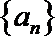
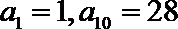
(2)对正整数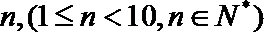
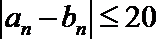
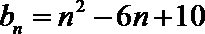
则数列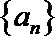
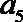
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
4.下列函数中,既是偶函数又在区间(0,+∞)上单调递增的是
正确答案
解析
显然y= -
y=-x2是偶函数,在区间(0,+∞)上单调递减,所以B不正确;
y=|x+1|是非奇非偶函数,在(0,+∞)上单调递增,所以D不正确;
对于C,因为



考查方向
解题思路
1.先根据函数的图像判断A、B、D选项的单调性和奇偶性; 2.利用偶函数的定义判断(C)中函数y=e一x+ex的奇偶性,然后利用导数确定其单调性。
易错点
1.对于函数y=e一x+ex的奇偶性不会判断;
2.函数y=e一x+ex的单调性判断不出来导致出错。
知识点
6.已知函数f(x)= 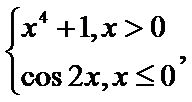
正确答案
解析
当x=1,f(1)=2,当x=-1,f(-1)=cos(-2)=cos2.所以A错。事实上,在不对称的区间上都是没有奇偶性的;
函数y=cos2x在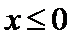
函数y=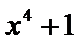
函数y=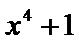
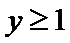
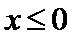
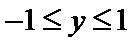
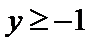
A选项不正确,B选项不正确,C选项不正确,所以选D选项。
考查方向
解题思路
1.对每一个选项进行判断即可;
2.也可以画出图像,直接判断。
A选项不正确, B选项不正确, C选项不正确,D选项正确。
易错点
1、本题不容易想到在x>0时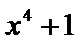
2、对于cos2x在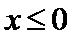
3、整个函数在定义域中的值域是求它们的交集容易出错。
知识点
3. 下列函数中,在区间
正确答案
解析
A满足在
考查方向
解题思路
直接判断各函数的单调性
易错点
对几个基本函数的图像不熟悉,指数函数和对数函数的性质不熟导致出错
知识点
6.下列函数中,既是奇函数,又在区间
正确答案
解析
A选项是奇函数,在区间


D选项是奇函数,在区间
考查方向
本题主要考查了函数的性质:奇偶性、单调性/函数的性质的综合考查在高考中经常出现,主要涉及区间转换法求解析式、比较大小、求参数取值或范围、解不等式等,主要考查单调性、奇偶性、对称性的综合应用,属于中档题。
解题思路
知识点
正确答案
知识点
扫码查看完整答案与解析