- 二次函数在闭区间上的最值
- 共44题
9.如果函数

正确答案
解析



















考查方向
解题思路
先根据是否是二次函数分类,然后



易错点
1.不能将题中给出的函数正确分类;
分类后想不到利用基本不等式导致没有思路。
知识点
1.已知



正确答案
解析
因为
所以
故可分别以OA,OB所在的直线为x轴,y轴建立直角坐标系,
则

故

又点C在∠AOB内,
且∠AOC=30°,
所以tan 30°
所以
故选B.
知识点
10.若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是
正确答案
解析
当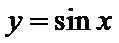
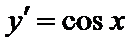
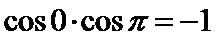
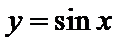
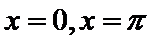
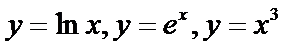
考查方向
解题思路
通过导数验证函数图像上存在两点的导数值乘积等于-1
易错点
新定义问题的理解,注意本题实质上是检验函数图像上存在两点的导数值乘积等于-1.
知识点
12.已知函数f(x+2)是偶函数,且当x>2时满足xf '(x)>2f '(x)+f(x)),则()
正确答案
解析
根据题意构造
所以

即就是
又由函数f(x+2)是偶函数可知f(x)关于
所以
故选A
考查方向
解题思路
1、由题函数f(x+2)是偶函数可知f(x)关于
2、根据题意构造


易错点
1、本题不易想到函数f(x+2)是偶函数可知f(x)关于
2、本题不容易理解xf '(x)>2f '(x)+f(x))的意思,得不到函数模型,导致题目无法进行。
知识点
16.如图,一横截面为等腰梯形的水渠,因泥沙沉积,导致水渠截面边界呈抛物线型(图中虚线表示),则原始的最大流量与当前最大流量的比值为( )
正确答案
1.2
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析