- 正弦函数的奇偶性
- 共47题
在
15.求B；
16.若
正确答案
（Ⅰ）
解析
试题分析：本题属于三角恒等变换与正弦定理的综合应用问题，属于简单题，解三角函数题，首先从角进行分析，善于用已知角表示所求角，即注重角的变换.角的变换涉及诱导公式、同角三角函数关系、两角和与差公式、二倍角公式、配角公式等，选用恰当的公式，是解决三角问题的关键，明确角的范围，对开方时正负取舍是解题正确的保证.本题只要掌握相关的公式及性质，即可解决本题，具体解析如下：
试题解析：（Ⅰ）解：在
考查方向
解题思路
（Ⅰ）利用正弦定理，将边化为角：
易错点
忽略角的范围导致出现增解。
正确答案
（Ⅱ）
解析
试题分析：本题属于三角恒等变换与正弦定理的综合应用问题，属于简单题，解三角函数题，首先从角进行分析，善于用已知角表示所求角，即注重角的变换.角的变换涉及诱导公式、同角三角函数关系、两角和与差公式、二倍角公式、配角公式等，选用恰当的公式，是解决三角问题的关键，明确角的范围，对开方时正负取舍是解题正确的保证.本题只要掌握相关的公式及性质，即可解决本题，具体解析如下：
（Ⅱ）解：由
考查方向
解题思路
（Ⅱ）问题为“已知两角，求第三角”，先利用三角形内角和为
易错点
忽略角的范围导致出现增解。
14.在锐角三角形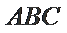
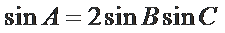
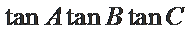
正确答案
8；
解析
由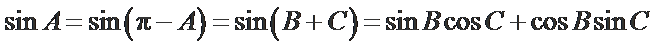
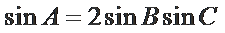
可得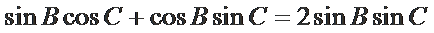
由三角形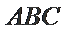
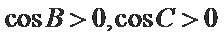
在（*）式两侧同时除以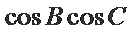
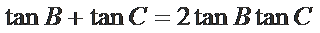
又
则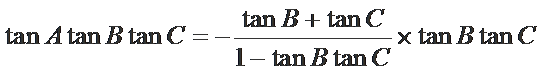
由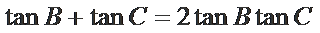
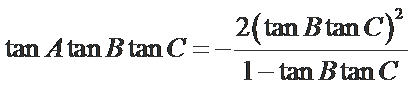
令
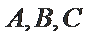
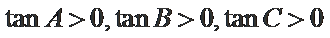
由(#)得
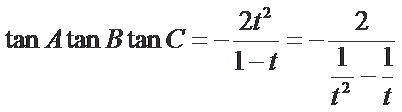
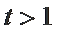
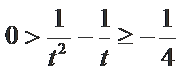
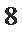
当且仅当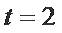
解得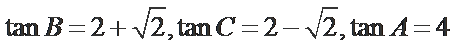
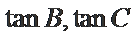
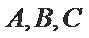
考查方向
解题思路
根据诱导公式、和差角公式化简，利用两边同除得到正切关系，应用正切公式的变形分析表示出
易错点
公式变形，函数关系转化，函数思想应用。
知识点
15. 在
(Ⅰ)求B；
(Ⅱ)若
正确答案
知识点
16．（本题满分14分）在△ABC中，内角A，B，C所对的边分别为a，b，c．已知b+c=2acos B．
（Ⅰ）证明：A=2B；
（Ⅱ）若cosB=
正确答案
（1）由正弦定理得
故
于是，
又
因此，
所以，
（2）由
故
知识点
4．△ABC的内角A、B、C的对边分别为a、b、C.已知
A
B
C2
D3
正确答案
知识点
5．若函数
正确答案
解析
考查方向
解题思路
利用三角变换转化为一角一函数
易错点
一角一函数的转化方法
知识点
5.下列函数中，最小正周期为π的奇函数是( )
Ay＝sin(2x＋
By＝cos(2x＋
Cy＝sin2x＋cos2x
Dy＝sinx＋cosx
正确答案
解析
A、B、C的周期都是π，D的周期是2π,但A中，y＝cos2x是偶函数，C中y＝
考查方向
解题思路
先将选项化简后利用三角函数的周期和奇偶性判断即可。
易错点
1利用诱导公式化简时没有注意奇偶导致出错；2不会利用辅助角公式化简C,D选项。
知识点
扫码查看完整答案与解析