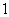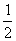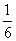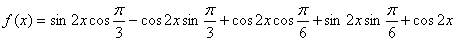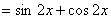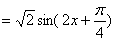- 正弦函数的定义域和值域
- 共98题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
若△



正确答案
解析

由正弦定理知
由余弦定理得 
知识点
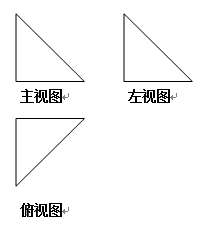
如图,一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为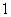
个几何体的体积为 ( )
正确答案
解析
由三视图还原几何体可知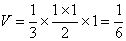
知识点
已知函数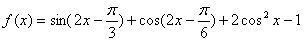
(1)求函数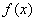
(2)求函数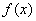
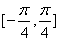
正确答案
见解析。
解析
(1)
所以函数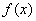
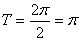
(2)因为
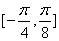

又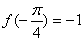
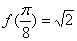
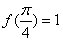
故函数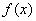
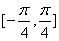
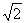
知识点
在
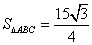

正确答案
8
解析
略
知识点
已知向量

(1)求 tanA的值;
(2)求函数
正确答案
见解析。
解析
(1)m·n=sinA-2cosA=0,得tanA=2.
(2)
当

所以f(x)的值域是
知识点
(几何证明选讲选做题)如图1,在平行四边形






正确答案
5
解析
略
知识点
已知函数
(1)求函数
(2)若

正确答案
(1)f(x)的最小正周期为2
(2)
解析
(1)由已知,f(x)=
所以f(x)的最小正周期为2

(2)由(1)知,f(
所以cos(
所以

知识点
设命题






正确答案
解析
知识点
设函数f(x)=sin2ωx+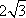

(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
正确答案
(1) 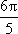
解析
(1)因为f(x)=sin2ωx-cos2ωx+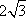
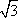
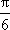
由直线x=π是y=f(x)图象的一条对称轴,可得sin(2ωπ-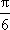
所以2ωπ-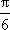
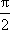
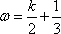
又ω∈(
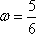
所以f(x)的最小正周期是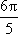
(2)由y=f(x)的图象过点(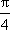
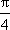
即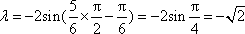
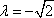
故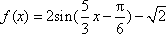
知识点
扫码查看完整答案与解析