绝对值三角不等式
共6题

· 绝对值三角不等式

绝对值三角不等式
共6题

热门试卷

X 查看更多试卷

题型：填空题

填空题 · 5 分

13．已知函数f(x)＝|x－2|，若a≠0，且a，b∈R，都有不等式成立，则实数x的取值范围是。

正确答案

[0,4]

解析

解析已在路上飞奔，马上就到！

知识点

不等式恒成立问题绝对值三角不等式

题型：填空题

填空题 · 5 分

若存在实数使成立，则实数的取值范围是（）。

正确答案

解析

表示在数轴上，a到1的距离小于等于3，即，

则

知识点

绝对值三角不等式

题型：简答题

简答题 · 13 分

已知集合，对于，，定义；

；与之间的距离为。

（1）当时，设，，若，求；

（2）（ⅰ）证明：若，且，使，则；

（ⅱ）设，且，是否一定，使？

说明理由；

（3）记，若，，且，求的最大值。

正确答案

见解析

解析

（1）解：当时，由，

得，即。

由，得，或。 ………………3分

（2）（ⅰ）证明：设，，。

因为，使，

所以，使得，

即，使得，其中。

所以与同为非负数或同为负数。 ………………5分

所以

。 ………………6分

（ⅱ）解：设，且，此时不一定，使得

。 ………………7分

反例如下：取，，，

则，，，显然。

因为，，

所以不存在，使得。 ………………8分

（3）解法一：因为，

设中有项为非负数，项为负数，不妨设时；时，。

所以

因为，

所以，整理得。

所以。……………10分

因为

；

又，

所以

。

即。 ……………12分

对于，，有，，且，

。

综上，的最大值为。 ……………13分

解法二：首先证明如下引理：设，则有。

证明：因为，，

所以，

即。

所以

。 ……………11分

上式等号成立的条件为，或，所以。 ……………12分

对于，，有，，且，

。

综上，的最大值为。 ……………13分

知识点

平行向量与共线向量分组转化法求和进行简单的合情推理绝对值三角不等式

题型：简答题

简答题 · 10 分

选修4—5：不等式选讲

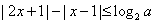
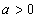
已知关于x的不等式（其中）。

（1）当a=4时，求不等式的解集；

（2）若不等式有解，求实数a的取值范围。

正确答案

见解析。

解析

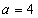
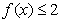
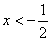
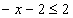
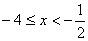
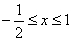
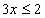
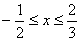
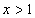
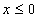
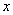
解析：（1）当时，，

时，，得（1分）

时，，得（2分）

时，，此时不存在（3分）

∴不等式的解集为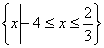（5分）

（2）略

知识点

绝对值三角不等式

题型：填空题

填空题 · 5 分

若关于实数x的不等式|x－5|＋|x＋3|＜a无解，则实数a的取值范围是________。

正确答案

（－∞，8]

解析

方法一：设f（x）＝|x－5|＋|x＋3|＝可求得f（x）的值域为[8，＋∞），因为原不等式无解，只需a≤8，故a的取值范围是（－∞，8]。

方法二：由绝对值不等式，得|x－5|＋|x＋3|≥|（x－5）－（x＋3）|＝8，

∴不等式|x－5|＋|x＋3|＜a无解时，a的取值范围为（－∞，8]

知识点

绝对值三角不等式绝对值不等式的解法

继续学习学习下一知识点

下一知识点 : 绝对值不等式的解法

百度题库 > 高考 > 理科数学 > 绝对值三角不等式

扫码查看完整答案与解析