- 由其它方法求数列的通项公式
- 共25题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
已知等差数列






(1)求数列
(2)求数列

(3)把集合


正确答案
见解析
解析
(1)设等比数列



(2)根据数列{an}和数列

所以S50=
(3)据集合B中元素2,8,32,128





证明如下:

若

同理,b2n+2-b2n=22n+1-22n-1=2×4n-2×4n-1=3×2×4n-1,即b2n+2=b2n+3×2×4n-1,因为“3×2×4n-1” 数列

当n=1时,显然b2=2

即得b2n

知识点
已知数列




(1)求
(2)求数列
(3)设数列






正确答案
见解析
解析
(1)由于

(2)由已知可知

因为

于是 

所以 
(3)
要比较


由

故
从而 
因此


设
则
故
又

所以对于任意 

从而
所以
即 
知识点
成等差数列的三个正数的和等于15,并且这三个数分别加上2、5、13后成为等比数列{bn}中的b3、b4、b5.
(1)求数列{bn}的通项公式;
(2)数列{bn}的前n项和为Sn,求证:数列
正确答案
见解析。
解析
(1)设成等差数列的三个正数分别为a-d,a,a+d.
依题意,得a-d+a+a+d=15.解得a=5.
所以{bn}中的b3,b4,b5依次为7-d,10,18+d.
依题意,有(7-d)(18+d)=100,
解得d=2或d=-13(舍去)。
故{bn}的第3项为5,公比为2.
由b3=b1·22,即5=b1·22,解得b1=
所以{bn}是以

(2)证明:由(1)得数列{bn}的前n项和
,即Sn+
所以
因此

知识点
已知正项数列






(1) 求数列

(2)设




正确答案
见解析。
解析
(1)由

由于

由



∴数列

(2)方法一:∵
∴
【方法二:∵
知识点
已知向量


(1)求数列
(2)若数列




正确答案
见解析。
解析
(1)






(2)







知识点
已知变量x,y,满足约束条件
正确答案
解析
略
知识点
已知数列{an},an+1=an+2,a1=1,数列{

正确答案
18
解析
∵ an+1=an+2,a1=1,
∴ an+1﹣an=2,
∴ 数列{an}是以1为首项,以2为公差的等差数列,
∴ an=1+2(n﹣1)=2n﹣1,
∴ 


∴
=
由数列{



知识点
设a, b, c均为不等于1的正实数, 则下列等式中恒成立的是()
正确答案
解析
a, b,c≠1. 考察对数2个公式:
对选项A: 
对选项B: 
对选项C: 
对选项D: 
所以选B
知识点
设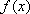
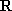
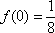
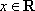
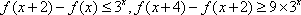
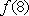
正确答案
解析
略
知识点
扫码查看完整答案与解析