- 直线方程和两条直线的位置关系
- 共550题
13.如图，AB是圆的直径，弦CD与AB相交于点E，BE=2AE=2，BD=ED，则线段CE的长为__________.
正确答案
知识点
5.圆（x+1）2+y2=2的圆心到直线y=x+3的距离为
A1
B2
C
D2
正确答案
知识点
12.已知圆C的圆心在x轴的正半轴上，点
正确答案
知识点
22.选修4-1：几何证明选讲
如图，△OAB是等腰三角形，∠AOB=120°.以O为圆心，
(I)证明：直线AB与⊙O相切；
(II)点C，D在⊙O上，且A，B，C，D四点共圆，证明：AB∥CD.
选修4—4：坐标系与参数方程
在直线坐标系xOy中，曲线C1的参数方程为
（I）说明C1是哪一种曲线，并将C1的方程化为极坐标方程；
（II）直线C3的极坐标方程为θ=α0，其中α0满足tanα0=2，若曲线C1与C2的公共点都在C3上，求a。
选修4—5：不等式选讲
已知函数f(x)= ∣x+1∣-∣2x-3∣.
（I）在答题卡第（24）题图中画出y= f(x)的图像；
（II）求不等式∣f(x)∣﹥1的解集。
正确答案
22(Ⅰ）设
因为
在
(2)设CD中点为Q，四边形ABCD外接圆圆心为O′.
连结OC,OD,O′C,O′D.
由OC=OD,知OQ⊥CD
由O′C=O′D,知O′Q⊥CD
∴O′,O,Q三点共线
同理，O,O′,P三点共线，
∴Q,O,O′,P四点共线
即PQ过点O，且PQ⊥AB, PQ⊥CD
∴AB//CD
23(1)
∴曲线
曲线
（2）曲线
①曲线
∵曲线
∴
24（Ⅰ）令x+1=0，2x-3=0 ∴x=-12；x=
∴f(x)=
作出草图
（Ⅱ）令
由图像知
知识点
2．圆心为
A
B
C
D
正确答案
解析
由题意可得圆的半径为
考查方向
解题思路
本题主要考查的是圆的标准方程，属于容易题．解题时一定要抓住重要字眼“过原点”，否则很容易出现错误．解本题需要掌握的知识点是圆的标准方程，即圆心
易错点
直线过原点
知识点
5.圆（x+1）2+y2=2的圆心到直线y=x+3的距离为
A1
B2
C
D2
正确答案
解析
圆心(-1,0) 直线为x-y+3=0 由点到线的距离公式得：
考查方向
解题思路
由题意得圆心，利用点到线距离公式计算
易错点
注意圆心的坐标符号
知识点
12. 如图，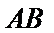
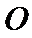
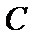
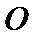
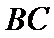
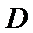
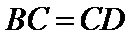
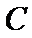
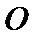
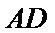
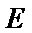
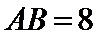
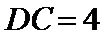
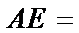
正确答案
3
解析
由题可知，a5=3a1+2a3，q4=3+2q2，q2=3，则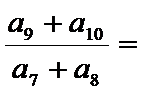
考查方向
解题思路
表示等差数列，表示首项与公比的关系，代入即可得到结果。
易错点
本题易在表示等差数列时发生错误。
知识点
设O为坐标原点，
Ax±
B
Cx±
D
正确答案
解析
选D，本题将解析几何与三角知识相结合，主要考察了双曲线的定义、标准方程，几何图形、几何性质、渐近线方程，以及斜三角形的解法，属中档题
知识点
过点P(1,1)的直线将圆形区域{(x，y)|x2＋y2≤4}分为两部分，使得这两部分的面积之差最大，则该直线的方程为( )
正确答案
解析
当OP与该直线垂直时，符合题意；此时kOP＝1，故所求直线斜率k＝－1.又已知直线过点P(1,1)，因此，直线方程为y－1＝－(x－1)，即x＋y－2＝0.
知识点
11.函数
正确答案
0
解析
考查方向
本题主要考查了导数的几何意义/导数的几何意义是高频考点，主要涉及求切线方程、求参数。
解题思路
易错点
易求错函数的导函数。
知识点
扫码查看完整答案与解析