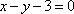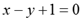- 直线方程和两条直线的位置关系
- 共550题
经过点















(1)求轨迹
(2)证明:
(3)若点




正确答案
见解析。
解析
(1)方法1:设动圆圆心为

整理,得


方法2:设动圆圆心为




根据抛物线的定义可知,动点
且其中定点

所以动圆圆心

(2)由(1)得


设点


由题意知点


则
即
因为

由于

所以
(3)方法1:由点



不妨设点




由
解得点

所以
由(2)知

所以△

解得
当



直线


当



直线


方法2:由点



由(2)知


由(2)知

所以
即
由(2)知
不妨设点


因为
同理
以下同方法1。
知识点
如图,已知椭圆C:


(1)求椭圆C的方程;
(2)过点


正确答案
见解析。
解析
(1)∵△AF1F2的周长为
∴

又

∴椭圆C的方程为
(2)由题意知,直线l的斜率必存在,
设其方程为
由
得
则
由
∴

设点R的坐标为(

得
∴
解得
而
∴
故点R在定直线
知识点
若直线

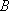

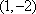
正确答案
解析
略
知识点
曲线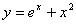
正确答案
解析
略
知识点
已知两定点





①


正确答案
①④
解析
略
知识点
已知圆










(1)求直线
(2)求圆
正确答案
见解析。
解析
(1)(法一)∵点

∴直线


(法二)当直线

当直线




则圆心




∴直线

(2)设圆



∴圆

∵圆






整理得:


∵

∴圆

知识点
过点(﹣1,0)与函数f(x)=ex(e是自然对数的底数)图象相切的直线方程是 。
正确答案
y=x+1
解析
设切点为(a,ea)
∵f(x)=ex,∴f′(x)=ex,
∴f′(a)=ea,
所以切线为:y﹣ea=ea(x﹣a),代入点(﹣1,0)得:
﹣ea=ea(﹣1﹣a),
解得a=0
因此切线为:y=x+1。
知识点
过点M(1 ,2)的直线l与圆

正确答案
解析
略
知识点
我们把具有公共焦点、公共对称轴的两段圆锥曲线弧合成的封闭曲线称为“盾圆”。
如图,“盾圆






(1)求椭圆的方程;
(2)是否存在过







正确答案
见解析
解析
(1)由


又


(2) 设直线

联立


联立


8分


整理得
若



同理

知识点
椭圆



(1)求椭圆的方程;
(2)过




正确答案
(1)
(2)y=x-1或y=-x-1
解析
(1)设右焦点为




又离心率



故椭圆方程为
(2)设





易知当直线的斜率不存在或斜率为0时,①不成立,
于是设的方程为



因为
于是

由①③得,



所以直线的方程是

知识点
扫码查看完整答案与解析