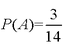- 随机事件及其概率
- 共412题
已知高二某班学生语文与数学的学业水平测试成绩抽样统计如下表,若抽取学生n人,成绩分为A(优秀)、B(良好)、C(及格)三个等级,设x,y分别表示语文成绩与数学成绩,例如:表中语文成绩为B等级的共有20+18+4=42人,已知x与y均为B等级的概率是0.18。
(1)求抽取的学生人数;
(2)设该样本中,语文成绩优秀率是30%,求a,b值;
(3)已知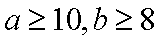
正确答案
(1)100(2)17(3)
解析
解析:
(1)由题意可知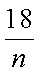
(2)由(1)知n=100,所以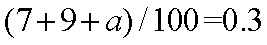
而7+9+a+20+18+4+5+6+b=100,故b=17. ………………6分
(3)设“语文成绩为A等级的总人数比语文成绩为C等级的总人数少”为事件A,
由(2)易知a+b=31,且a≥10,b≥8, ………………7分
满足条件的(a,b)有
(10,21),(11,20),(12,19),(13,18), (14,17),
(15,16),(16,15
(20,11),(21,10),(22,9),(23,8),共有14组, ………………10分
其中b+11
则所求概率为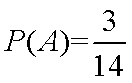

知识点

(1)写出频率分布直方图中的
(2)记甲种酸奶与乙种酸奶日销售量(单位:箱)的方差分别为



(3)假设同一组中的每个数据可用该组区间的中点值代替,试估计乙种酸奶在未来一个月(按30天计算)的销售总量.
正确答案
见解析
解析
(1)

(2)
(3)乙种酸奶平均日销售量为:

乙种酸奶未来一个月的销售总量为:
知识点
在平面直角坐标系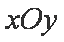
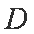

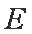
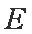

正确答案
解析
略
知识点
有甲、乙、丙、丁四位歌手参加比赛,其中只有一位获奖,有人走访了四位歌手,甲说:“是乙或丙获奖”,乙说:“甲、丙都未获奖”,丙说:“我获奖了”,丁说:“是乙获奖了”.四位歌手的话只有两句是对的,则获奖的歌手是 。
正确答案
答案:丙
解析
略
知识点
为大力提倡“厉行节约,反对浪费”,某市通过随机询问100名性别不同的居民是否能做到“光盘”行动,得到如下的列联表:
附:
参照附表,得到的正确结论是
正确答案
解析
略
知识点
对一批共50件的某电器进行分类检测,其重量(克)统计如下:
规定重量在82克及以下的为“A”型,重量在85克及以上的为“B”型,已知该批电器有“A”型2件
(1)从该批电器中任选1件,求其为“B”型的概率;
(2)从重量在[80,85)的5件电器中,任选2件,求其中恰有1件为“A”型的概率。
正确答案
见解析
解析
解:(1)设“从该批电器中任选1件,其为”B”型”为事件A1,
则
所以从该批电器中任选1件,求其为”B”型的概率为
(2)设“从重量在[80,85)的5件电器中,任选2件电器,求其中恰有1件为”A”型”为事件A2,记这5件电器分别为a,b,c,d,e,其中”A”型为a,b,从中任选2件,所有可能的情况为ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种
其中恰有1件为”A”型的情况有ac,ad,ae,bc,bd,be,共6种
所以

知识点
某学校为了增强学生对数学史的了解,提高学生学习数学的积极性,举行了一次数 学史知识竞赛,其中一道题是连线题,要求将4名数学家与他们所著的4本著作一 对一连线,规定:每连对一条得5分,连错一条得-2分.某参赛者随机用4条线把 数学家与著作一对一全部连接起来
(1)求该参赛者恰好连对一条的概率。
(2)求该参赛者得分不低于6分的概率。
正确答案
(1)
解析
记4名数学家分别为

(4分)
其中恰好连对一条的情形有如下8种:
恰好连对两条的情形有如下6种:
全部连对的情形只有1种:

(1) 恰好连对1条的概率为
(2) 得分不低于6分即全部连对或恰好连对2条的概率为
知识点
某高中共有
的方法从中抽取
正确答案
16
解析
略
知识点
已知函数
(1)从区间





(2)若连续掷两次骰子(骰子六个面上标注的点数分别为






正确答案
见解析
解析
解:(1)







(2)由已知:






当





当



而基本事件总数为

知识点
某在元宵节活动上,组织了“摸灯笼猜灯谜”的趣味游戏.已知在一个不透明的箱子内放有大小和形状相同的标号分别为1,2,3的小灯笼若干个,每个灯笼上都有一个谜语,其中标号为1的小灯笼1个,标号为2的小灯笼2个,标号为3的小灯笼n个.若参赛者从箱子中随机摸取1个小灯笼进行谜语破解,取到标号为3的小灯笼的概率为
(1)求n的值;
(2)从箱子中不放回地摸取2个小灯笼,记第一次摸取的小灯笼的标号为a,第二次摸取的小灯笼的标号为b.记“
正确答案
见解析
解析
(1)由题意,
(2)记标号为2的小灯笼为

(1, 





















知识点
扫码查看完整答案与解析