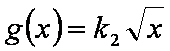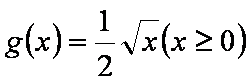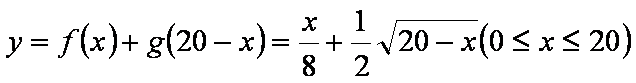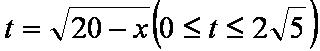- 随机事件及其概率
- 共412题
设实数x,y满足

正确答案
解析
约束条件

所以正方形的面积为2.圆


知识点
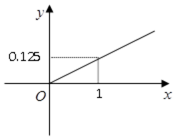
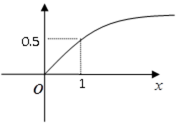
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比。已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图)
(1)分别写出两种产品的收益与投资的函数关系。
(2)该家庭现有20万元资金,全部用于理财投资,问:怎么分配资金能使投资获得最大收益,其最大收益是多少万元?
正确答案
见解析
解析
(1)设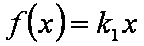
所以 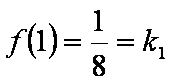
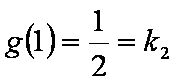
即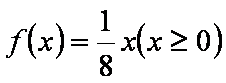
(2)设投资债券类产品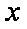
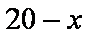
依题意得:
令
则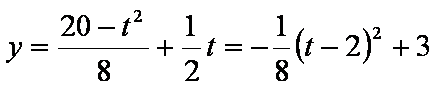
所以当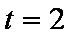
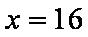
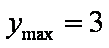
知识点
第11届全国人大五次会议于2012年3月5日至3月14日在北京召开,为了搞好对外宣传工作,会务组选聘了16名男记者和14名记者担任对外翻译工作,调查发现,男、女记者中分别有10人和6人会俄语。
(1)根据以上数据完成以下2X2列联表:
并回答能否在犯错的概率不超过0。10的前提下认为性别与会俄语有关?
(2)会俄语的6名女记者中有4人曾在俄罗斯工作过,若从会俄语的6名女记者中随机抽
取2人做同声翻译,则抽出的2人都在俄罗斯工作过的概率是多少?
正确答案
见解析。
解析
(1)如下表:
假设:是否会俄语与性别无关,由已知数据可求得

所以在犯错的概率不超过0。10的前提下不能判断会俄语与性别有关。
(2)会俄语的6名女记者,分别设为A,B,C,D,E,F,其中A,B,C,D曾在俄罗斯工作过。
则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD, BE,BF,CD,CE, CF,DE,
DF,EF 共15种,
其中2人都在俄罗斯工作过的是AB,AC,AD,BC,BD,CD共6种,
所以抽出的女记者中,2人都在俄罗斯工作过的概率是P=
知识点
时维壬辰,序属仲春,值春耕播种时机,某中学生物研究性学习小组对春季昼夜温差大小与水稻发芽率之间的关系进行研究,记录了实验室4月10日至4月14日的每天昼夜温差与每天每50颗稻籽浸泡后的发芽数,得到如下资料:
(1)从4月10日至4月14日中任选2天,记发芽的种子数分别为m,n,求事件“m,n均小于14”的概率;
(2)根据表中的数据可知发芽数y(颗)与温差x(oC)呈线性相关,请求出发芽数y关于温差x的线性回归方程
(参考公式:回归直线方程式

正确答案
见解析。
解析
(1)m,n构成的基本事件(m,n)有:(11,13),(11,14),(11,16),(11,12),(13,14),(13,16),(13,12),(14,16),(14,12),(16,12),共有10个。
其中“m,n均小于14”的有3个,其概率为
(2)∵
∴
于是,
故所求线性回归方程为 
知识点
某校一研究性学习小组对宿州市工薪阶层关于“楼市限购令”态度进行调查,随机抽调了50人,他们月收入频数分布及对“楼市限购令”赞成人数如下表:
(1)完成下图的月收入频率分布直方图及2×2列联表:
(2)若从月收入(单位:百元)在

正确答案
见解析。
解析
(1)各组的频率分别是0.1,0.2,0.3,0.2,0.1,0.1,所以频率分布直方图中各组的纵坐标分别是0.01,0.02,0.03,0.02,0.01,0.01故频率分布直方图如图.
(2)设月收入在[15,25)内的5人分别为

月收入在[65,75)内的5人分别为


























故选中的2人中至少有1人赞成“楼市限购令”的概率
知识点
某校有教职工
(1)随机抽取一人,是35岁以下的概率为

(2)从50岁以上的6人中随机抽取两人,求恰好只有一位是研究生的概率。
正确答案
见解析
解析
解:(1)由已知得:
故
(2)将50岁以上的6人进行编号:四位本科生为:1,2,3,4,两位研究生为5,6。
从这6人中任取2人共有15种等可能发生的基本事件,
分别为:12,13,14,15,16,23,24,25,26,34,35,36,45,46,56]
其中恰好有一位研究生的有8种,分别为:15,16,25,26,35,36,45,46
故所求的概率为:
知识点
有一批货物需要用汽车从城市甲运至城市乙,已知从城市甲到城市乙只有两条公路,且通过这两条公路所用的时间互不影响,据调查统计,通过这两条公路从城市甲到城市乙的200辆汽车所用时间的频数分布如下表:
(1)为进行某项研究,从所用时间为12天的60辆汽车中随机抽取6辆。
①若用分层抽样的方法抽取,求从通过公路1和公路2的汽车中各抽取几辆;
②若在①的条件下抽取的6辆汽车中,再任意抽取两辆汽车,求这两辆汽车至少有一辆通过公路1的概率。
(2)假设汽车A只能在约定日期(某月某日)的前11天出发,汽车B只能在约定日期的前12天出发,为了尽最大可能在各自允许的时间内将货物运往城市乙,估计汽车A和汽车B应如何选择各自的路径。
正确答案
见解析
解析
(1)①公路1抽取6×
公路2抽取6×
②通过公路1的两辆汽车分别用A1、A2表示,通过公路2的4辆汽车分别用B1、B2、B3、B4表示,
任意抽取2辆汽车共有15种可能的结果:(A1,A2),(A1,B1),(A1,B2),(A1,B3),(A1,B4),(A2,B1),(A2,B2),(A2,B3),(A2,B4),(B1,B2),(B1,B3),(B1,B4),(B2,B3), (B2,B4),(B3,B4)
其中至少有1辆经过公路1的有9种,
所以至少有1辆经过1号公路的概率
(2)频率分布表如下:
设C1、C2分别表示汽车A在前11天出发选择公路1、2将货物运往城市乙;D1、D2分别表示汽车B
在前12天出发选择公路1、2将货物运往城市乙。
P(C1)=0.2+0.4=0.6,P(C2)=0.1+0.4=0.5,
∴汽车A应选择公路1.
知识点



正确答案
解析
点
知识点
一工厂生产甲, 乙, 丙三种样式的杯子,每种样式均有500ml和700ml两种型号,
某天的产量如右表(单位:个):
按样式进行分层抽样,在该天生产的杯子中抽取100个,其中有甲样式杯子25个.
(1)求z的值;
(2)用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,从这个样本中任取2个杯子,求至少有1个500ml杯子的概率。
正确答案
见解析
解析
解: (1)设该厂本月生产的乙样式的杯子为n个,在丙样式的杯子中抽取x个,由题意得, 
则100-40-25=

故z=2500
(2)设所抽样本中有m个500ml杯子,
因为用分层抽样的方法在甲样式杯子中抽取一个容量为5的样本,
所以
也就是抽取了2个500ml杯子,3个700ml杯子,分别记作S1,S2;B1,B2,B3,则从中任取2个的所有基本事件为(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,其中至少有1个500ml杯子的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),所以从中任
至少有1个500ml杯子的概率为

知识点
近年来空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重,大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对入院50人进行了问卷调查,得到如下的列联表:
(1)用分层抽样的方法在患心肺疾病的人群中抽6人,其中男性抽多少人?
(2)在(1)中抽取的6人中选2人,求恰有一名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量
参考公式与临界值表:

正确答案
(1)4
(2)
(3)8.333,有
解析
(1)男性应该抽取
(2)在上述抽取的6名患者中, 女性的有2人,男性4人. 女性2人记

则从6名患者任取2名的所有情况为: 














其中恰有1名女性情况有: 







故上述抽取的6人中选2人恰有一名女性的概率概率为
(3)


知识点
扫码查看完整答案与解析