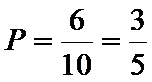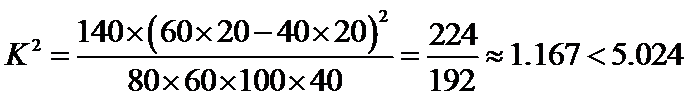- 随机事件及其概率
- 共412题
18. 现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了100人,他们月收入(单位百元)的频数分布及对“楼市限购令”赞成人数如下表.
(Ⅰ)由以上统计数据填下面

(Ⅱ)若对月收入在


(下面的临界值表供参考)


正确答案
(1)有95%的把握认为“月收入以
对“楼市限购令”的态度有差异;(2)
解析
试题分析:本题属于数列中的基本问题,题目的难度不大,
(1)直接按照步骤来求,先将表格补充完整,再代入公式计算出k的观测值,再下结论
(2)利用古典概型的公式来计算.
(Ⅰ)解:列联表补充如下
因为
又

对“楼市限购令”的态度有差异.
(Ⅱ)解:在上述抽取的6人中, 月收入在

月收入在



则从6人任取2名的所有情况为: 













共15种情况,
其中恰有1名月收入在








故上述抽取的6人中选2人,恰有一名月收入在
考查方向
解题思路
本题考查独立性检验和古典概型,解题步骤如下:
先将表格补充完整,再代入公式计算出k的观测值,再下结论。
利用古典概型的公式来计算。
易错点
第1问不知道怎么下结论,第2问列举不全。
知识点
一辆小客车上有5个座位,其座位号为1,2,3,4,5,乘客P1,P2,P3,P4,P5的座位号分别为1,2,3,4,5,他们按照座位号顺序先后上车,乘客P1因身体原因没有坐自己号座位,这时司机要求余下的乘客按以下规则就坐:如果自己的座位空着,就只能坐自己的座位.如果自己的座位已有乘客就坐,就在这5个座位的剩余空位中选择座位.
18.P1坐到了3号座位,其他乘客按规则就座,则此时共有4种坐法.下表给出其中两种坐法,请填入余下两种坐法(将乘客就坐的座位号填入表中空格处)
19.P1坐到了2号座位,其他乘客按规则就坐,求乘客P1坐到5号座位的概率.
正确答案
余下两种坐法如下表所示
解析
见答案
考查方向
解题思路
弄清题意后直接将可能的情况全部列举出来即可;
易错点
.对于题意理解有困难,不知道说的是什么导致没有思路。
正确答案

解析
若乘客P1做到了2号座位,其他乘客按规则就坐
则所有可能坐法可用下表表示为
于是,所有可能的坐法共8种
设“乘客P5坐到5号座位”为事件A,则事件A中的基本事件的个数为4
所以PA.=
答:乘客P5坐到5号座位的概率为
考查方向
解题思路
直接将可能的情况列举出来,后利用古典概型的概率公式求解即可。
易错点
.对于题意理解有困难,不知道说的是什么导致没有思路。
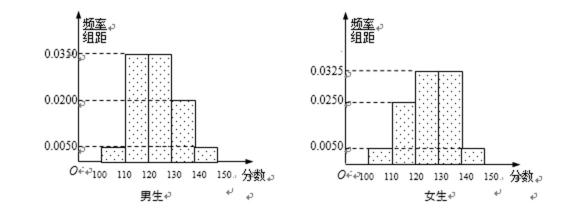
18.某学校高三年级有学生500人,其中男生300人,女生200人,为了研究学生的数学成绩是否与性别有关,现采用分层抽样的方法,从中抽取了100名学生,先统计了他们期中考试的数学分数,然后按性别分为男、女两组,再将两组学生的分数分成5组:[100,110),[110,120),[120,130),[130,140),[140,150]分别加以统计,得到如图所示的频率分布直方图.
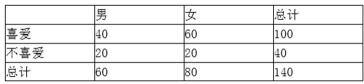
(1)从样本中分数小于110分的学生中随机抽取2人,求两人恰好为一男一女的概率;
(2)若规定分数不小于130分的学生为“数学尖子生”,
附:
正确答案
(1)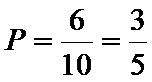
解析
试题分析:本题属古典概型及独立性检验,(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
试题解析:(1)解:由已知得,抽取的100名学生中,男生60名,女生40名
分数小于等于110分的学生中,
男生人有60×0.05 = 3(人),记为A1,A2,A3;女生有40×0.05 = 2
从中随机抽取2名学生,所有的可能结果共有10种,
(A2,A3),(A1,B1),(A1,B2),(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2)
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),
故所求的概率
(2)解:由频率分布直方图可知,
在抽取的100名学生中,男生 60×0
据此可得2×2列联表如下:
所以得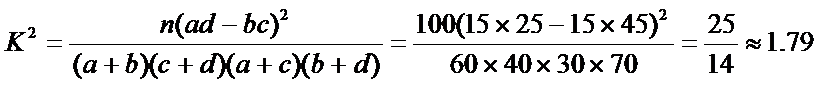
因为1.79 < 2.706.
所以没有90%的把握认为“数学尖子生与性别有关”.
考查方向
解题思路
本题考查了古典概型及独立性检验,解题步骤如下:(1)先根据分层抽样算出抽出的人数,然后利用古典概型的公式计算;(2)列出联表然后代入公式计算出k的观测值,然后下结论。
易错点
在找基本事件的个数的时候有可能遗漏或者重复。
知识点
8.已知下列三个命题:
①若两组数据的平均数相等,则它们的标准差也相等
②在区间
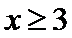
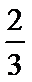
③直线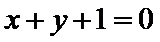
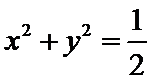
其中真命题的个数是( )
正确答案
解析
1)根据平均数、方差与标准差的性质可知①错误
2)根据与长度有关的几何概型可知正确为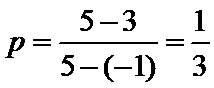
3)根据直线与圆的位置关系,圆心到直线的距离为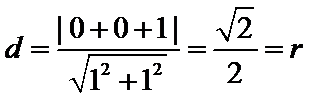
∴ 选B
考查方向
解题思路
直接法对每一个判断
1)根据平均数、方差与标准差的性质可知①错误
2)根据与长度有关的几何概型可知正确为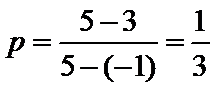
3)根据直线与圆的位置关系,圆心到直线的距离为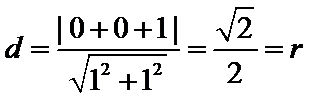
易错点
本题属于数学中的多选题,易错于对个别判断错误导致选择错误,
知识点
已知某中学高三文科班学生共有



(Ⅰ)如果从第




(Ⅱ)抽的
21.成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有


22.将



正确答案
(1)

解析
(Ⅰ)依题意,最先检测的3个人的编号依次为
(Ⅱ)由

因为

考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
正确答案
(2)
解析
(Ⅲ)由题意,知

故满足条件的



其中数学成绩为优秀的人数比及格的人数少有:


∴数学成绩优秀的人数比及格的人数少的概率为
考查方向
解题思路
1)第一问考察统计的知识,比较简单,直接由比例可得出
2)第二问中属于古典概型,较简单,直接列举出所有的情况,数出个数作商。
易错点
容易在找出满足条件的所有事件时丢掉。
某市为庆祝北京夺得











16.若电视台记者要从抽取的群众中选


17.已知第




正确答案
(Ⅰ)
解析
(Ⅰ)设第



被采访人恰好在第


∴估计被采访人恰好在第

考查方向
解题思路
根据题中给出的频率分布直方图求出第(1)问的答案;
易错点
列基本事件的个数时多数或少数。
正确答案
(Ⅱ)
解析
(Ⅱ)第


∴第


记第




从第



至少有一名女性群众包含
共
∴从第



考查方向
解题思路
求出各组中的群众人数,后数出所有的基本事件的个数和事件 至少有一名女性群众所包含的基本事件的个数相除即可。
易错点
列基本事件的个数时多数或少数。
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为

考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
17. 有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(I)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(II)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个
正确答案
见解析
解析
所以含有编号为2的球的概率
考查方向
解题思路
写出基本事件空间,并用古典概型的概率公式计算概率
易错点
本题易错在第一问分类不清
知识点
6. 在区间



正确答案
解析
命题“





考查方向
解题思路
由命题为真命题,可得
易错点
容易将区域画错
知识点
周立波是海派清口创始人和《壹周·立波秀》节目的主持人,他的点评视角独特,语言幽默犀利,给观众留下了深刻的印象.某机构为了了解观众对《壹周·立波秀》节目的喜爱程度,随机调查了观看了该节目的140名观众,得到如下的列联表:(单位:名)
19.从这60名男观众中按对《壹周·立波秀》节目是否喜爱采取分层抽样,抽取一个容量为6的样本,问样本中喜爱与不喜爱的观众各有多少名?
20,根据以上列联表,问能否在犯错误的概率不超过0.025的前提下认为观众性别与喜爱《壹周·立波秀》节目有关.(精确到0.001)
21.从19题中的6名男性观众中随机选取两名作跟踪调查,求选到的两名观众都喜爱《壹周·立波秀》节目的概率.
正确答案
喜爱的观众有4名;不喜爱的观众有2名.
解析
抽样比为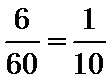
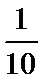
考查方向
解题思路
直接计算抽样比,即可算出喜爱与不喜爱的人数;
易错点
对“独立性检验的思想”不理解易出错
正确答案
不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
解析
假设:观众性别与喜爱无关,由已知数据可求得,
∴ 不能在犯错误的概率不超过0.025的前提下认为观众性别与喜爱有关.
考查方向
解题思路
直接代入公式计算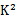
易错点
对“独立性检验的思想”不理解易出错
正确答案
0.4
解析
记喜爱的4名男性观众为a,b,c,d,不喜爱的2名男性观众为1
其中选到的两名观众都喜爱的事件有6个,
故其概率为
考查方向
解题思路
直接列出总事件及发生事件的情况,直接求比。
易错点
对“独立性检验的思想”不理解易出错
扫码查看完整答案与解析