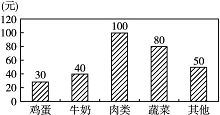- 随机事件及其概率
- 共412题
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
请你谈一谈对“不同生产方式以及生产工艺中,生产物流管理所采用的方法和手段是不同的。”这句话的理解。
正确答案
测试
如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0),B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点。
(1)求这3点与原点O恰好是正三棱锥的四个顶点的概率;
(2)求这3点与原点O共面的概率。
正确答案
(1) 
解析
从这6个点中随机选取3个点的所有可能结果是:
x轴上取2个点的有A1A2B1,A1A2B2,A1A2C1,A1A2C2,共4种,
y轴上取2个点的有B1B2A1,B1B2A2,B1B2C1,B1B2C2,共4种,
z轴上取2个点的有C1C2A1,C1C2A2,C1C2B1,C1C2B2,共4种。
所选取的3个点在不同坐标轴上有A1B1C1,A1B1C2,A1B2C1,A1B2C2,A2B1C1,A2B1C2,A2B2C1,A2B2C2,共8种。
因此,从这6个点中随机选取3个点的所有可能结果共20种。
(1)选取的这3个点与原点O恰好是正三棱锥的四个顶点的所有可能结果有:A1B1C1,A2B2C2,共2种,因此,这3个点与原点O恰好是正三棱锥的四个顶点的概率为
(2)选取的这3个点与原点O共面的所有可能结果有:A1A2B1,A1A2B2,A1A2C1,A1A2C2,B1B2A1,B1B2A2,B1B2C1,B1B2C2,C1C2A1,C1C2A2,C1C2B1,C1C2B2,共12种,因此,这3个点与原点O共面的概率为
知识点
设a∈[-2,0],已知函数
(1)证明f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增;
(2)设曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,且x1x2x3≠0.证明x1+x2+x3>
正确答案
见解析
解析
(1)设函数f1(x)=x3-(a+5)x(x≤0),f2(x)=
①f1′(x)=3x2-(a+5),由a∈[-2,0],从而当-1<x<0时,f1′(x)=3x2-(a+5)<3-a-5≤0,所以函数f1(x)在区间(-1,0]内单调递减。
②f2′(x)=3x2-(a+3)x+a=(3x-a)(x-1),由于a∈[-2,0],所以当0<x<1时,f2′(x)<0;当x>1时,f2′(x)>0.即函数f2(x)在区间[0,1)内单调递减,在区间(1,+∞)内单调递增。
综合①,②及f1(0)=f2(0),可知函数f(x)在区间(-1,1)内单调递减,在区间(1,+∞)内单调递增。
(2)由(1)知f′(x)在区间(-∞,0)内单调递减,在区间

因为曲线y=f(x)在点Pi(xi,f(xi))(i=1,2,3)处的切线相互平行,从而x1,x2,x3互不相等,且f′(x1)=f′(x2)=f′(x3),不妨设x1<0<x2<x3,由


可得


设g(x)=3x2-(a+3)x+a,则
由

所以x1+x2+x3>
设t=

因为a∈[-2,0],所以t∈
故x1+x2+x3>

知识点
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女。
(1)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(2)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
正确答案
(1)
(2)
解析
(1) 从甲校和乙校报名的教师中各任选1名,所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男),共9种;选出的2名教师性别相同的结果有(甲男1,乙男)、(甲男2, 乙男)、(甲女1, 乙女1)、(甲女1, 乙女2),共4种,所以选出的2名教师性别相同的概率为
(2)从报名的6名教师中任选2名,所有可能的结果为(甲男1,乙男)、(甲男2, 乙男)、(甲男1, 乙女1)、(甲男1, 乙女2)、(甲男2, 乙女1)、(甲男2, 乙女2)、(甲女, 乙女1)、(甲女, 乙女2) 、(甲女, 乙男) 、(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2),共15种;选出的2名教师来自同一学校的所有可能的结果为(甲男1, 甲男2)、(甲男1, 甲女)、(甲男2, 甲女)、(乙男, 乙女1)、(乙男, 乙女2)、(乙女1, 乙女2),共6种,所以选出的2名教师来自同一学校的概率为
知识点
若点(a,b)在

正确答案
解析
略
知识点
设函数



(1)求数列
(2)设



正确答案
(1)
解析
(I)
得:当

得:
(2)由(I)得:
当
当
当
得: 当
当
当
知识点
设A,B为直线y=x与圆x2+y2=1的两个交点,则|AB|=( )
正确答案
解析
由已知条件可知直线y=x过圆x2+y2=1的圆心,所以AB为圆x2+y2=1的直径,|AB|=2,故选D项
知识点
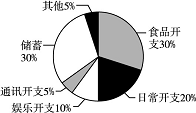
小波一星期的总开支分布如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为( )
正确答案
解析
由题图2知,小波一星期的食品开支为300元,其中鸡蛋开支为30元,占食品开支的10%,而食品开支占总开支的30%,所以小波一星期的鸡蛋开支占总开支的3%,故选C项
知识点
扫码查看完整答案与解析