- 随机事件及其概率
- 共412题
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立。
(1)求该地1位车主至少购买甲、乙两种保险中的1种的概率;
(2)求该地3位车主中恰有1位车主甲、乙两种保险都不购买的概率。
正确答案
(1) 0.8;(2)0.384
解析
记A表示事件:该地的1位车主购买甲种保险:
B表示事件:该地的1位车主购买乙种保险但不购买甲种保险。
C表示事件:该地的1位车主至少购买甲、乙两种保险中的1种;
D表示事件:该地的1位车主甲、乙两种保险都不购买;
E表示事件:该地的3位车主中恰有1位车主甲、乙两种保险都不购买。
(1)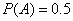
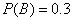
(2)D=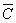
P(E)=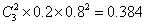
知识点
总体编号为01,02,…19,20的20个个体组成。利用下面的随机数表选取5个个体,选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为
正确答案
解析
从第5列和第6列选出的两位数依次为65,72,08,02,63,14,07,02,43,69,97,28,01,98,但编号必须不大于20的且不和前面重复的只能是08,02,14,07,01,选D
知识点
从3男3女共6名同学中任选2名(每名同学被选中的机会均等),这2名都是女同学的概率等于__________。
正确答案
解析
从3男,3女中任选两名,共有15种基本情况,而从3女中任选2名女同学,则有3种基本情况,故所求事件的概率为
知识点
如图,A地到火车站共有两条路径

(1)试估计40分钟内不能赶到火车站的概率;
(2 )分别求通过路径

(3)现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站,为了尽量大可能在允许的时间内赶到火车站,试通过计算说明,他们应如何选择各自的路径。
正确答案
见解析。
解析
(1)由已知共调查了100人,其中40分钟内不能赶到火车站的有12+12+16+4=44人,

(2 )选择

故由调查结果得频率为:
(3)用







由(2)知P(A1) =0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5, P(A1)


P(B1) =0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4=0.9,P(B2)>P(B1),
∴ 乙应选择路径L2.
知识点
某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售。如果当天卖不完,剩下的玫瑰花做垃圾处理。
(1)若花店一天购进17枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式。
(2)花店记录了100天
(i)假设花店在这100天内每天购进17枝玫瑰花,求这100天
(ii)若花店一天购进17枝玫瑰花,以100天记录的各需求量的频率作为各需求量发生的概率,求当天的利润不少于75元的概率。
正确答案
(1)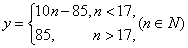
解析
(1)当日需求量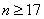
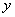
当日需求量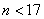
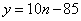
∴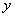
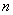
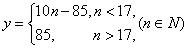
(2)(i)这100天中有10天的日利润为55元,20天的日利润为65元,16天的日利润为75元,54天的日利润为85元,所以这100天的平均利润为
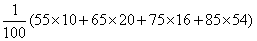
(ii)利润不低于75元当且仅当日需求不少于16枝,故当天的利润不少于75元的概率为
知识点
根据下列算法语句, 当输入x为60时, 输出y的值为()
正确答案
解析

知识点
某个不透明的袋中装有除颜色外其它特征完全相同的7个乒乓球(袋中仅有白色和黄色两种颜色的球),若从袋中随机摸一个乒乓球,得到的球是白色乒乓球的概率是
正确答案
解析
略
知识点
已知集合M={1,2,3,4},N={-2,2},下列结论成立的是( )
正确答案
解析
∵M={1,2,3,4},N={-2,2},∴M∩N={2}
知识点
在3张奖券中有一、二等奖各1张,另1张无奖,甲、乙两人各抽取1张,两人都中奖的概率是______________;
正确答案
解析
基本事件的总数是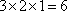
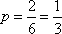
知识点
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率。
正确答案
(1)n=40
(2)
解析
(1)根据分层抽样按比例抽取,所以
解得
(2)35岁以下:
35岁以上:
设:将35岁以下4人标记为1、2、3、4,35岁以上1人标记为a.所有基本事件为:
其中满足条件得有

答:恰好有1个人在35岁以上(含35岁)的概率为
知识点
扫码查看完整答案与解析