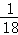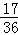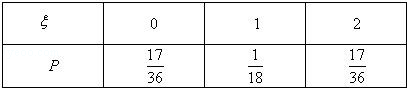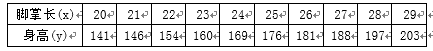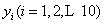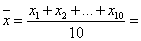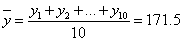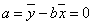- 随机事件及其概率
- 共412题
设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计)。
(1)求方程x2+bx+c=0有实根的概率;
(2)求ξ的分布列和数学期望;
正确答案
见解析。
解析
(1)由题意知本题是一个古典概型,试验发生包含的所有事件根据分步计数原理知是36,满足条件的事件是方程x2+bx+c=0有实根包括有一个实根,有两个实根,这两种结果是互斥的,根据互斥事件的概率公式得到结果。
(2)由题意知实根的个数只有三种结果,0、1、2,根据上一问的计算可以写出当变量取值时对应的概率,写出分布列,算出期望。
解:(1)由题意知:设基本事件空间为Ω,
记“方程x2+bx+c=0没有实根”为事件A,
“方程x2+bx+c=0有且仅有一个实根”为事件B,
“方程x2+bx+c=0有两个相异实数”为事件C
则Ω={(b,c)|b,c=1,2,3,4,5,6}
Ω是的基本事件总数为36个,
A={(b,c)|b2﹣4c<0,b,c=1,2,3,4,5,6},A中的基本事件总数为17个;
B={(b,c)|b2﹣4c=0,b,c=1,2,3,4,5,6},B中的基本事件总数为2个;
C={(b,c)|b2﹣4c>0,b,c=1,2,3,4,5,6},C中的基本事件总数为17个;
又因为B,C是互斥事件,
∴所求概率P=P(B)+P(C)=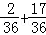
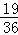
(2)由题意,ξ的可能取值为0,1,2,则
P(ξ=0)=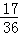
P(ξ=1)=
P(ξ=2)=
∴ξ的分布列为:
∴ξ的数学期望Eξ=0×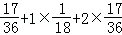
知识点
某次运动会在我市举行,为了搞好接待工作,组委会招募了16名男志愿者和14名女志愿者,调查发现,男、女志愿者中分别有10人和6人喜爱运动,其余不喜爱。
(1)根据以上数据完成以下2×2列联表:
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人能胜任翻译工作),抽取2名,则抽出的志愿者都能胜任翻译工作的概率是多少?
参考公式:
参考数据:
正确答案
见解析。
解析
(1)
(2)假设:是否喜爱运动与性别无关,由已知数据可求得:
因此,在犯错的概率不超过0.10的前提下不能判断喜爱运动与性别有关6分
(3)喜欢运动的女志愿者有6人,
设分别为A、B、C、D、E、F,其中A、B、C、D会外语,则从这6人中任取2人有AB,AC,AD,AE,AF,BC,BD,BE,BF,CD,CE,CF,DE,DF,EF,共15种取法,其中两人都会外语的有AB,AC,AD,BC,BD,CD,共6种。
故抽出的志愿者中2人都能胜任翻译工作的概率是
知识点
一般来说,一个人脚掌越长,他的身高就越高.现对10名成年人的脚掌长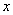
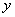
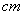
(1)在上表数据中,以“脚掌长”为横坐标,“身高”为纵坐标,作出散点图后,发现散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程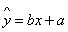
(2)若某人的脚掌长为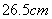
(3)在样本中,从身高180cm以上的4人中随机抽取2人作进一步的分析,求所抽取的2人中至少有1人身高在190cm以上的概率。
(参考数据: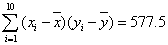
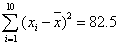
正确答案
见解析。
解析
(1)记样本中10人的“脚掌长”为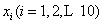

则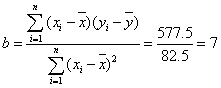
∵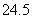
∴
∴
(2)由(20)知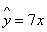
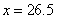
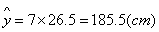
故估计此人的身高为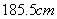
(3)将身高为181、188、197、203(cm)的4人分别记为A、B、C、D,
记“从身高180cm以上4人中随机抽取2人,所抽的2人中至少有1个身高在190cm以上”为事件A,
则基本事件有:(AB)、(AC)、(AD)、(BC)、(BD)、(CD),总数6,
A包含的基本事件有:(AC)、(AD)、(BC)、(BD)、(CD),个数5,
所以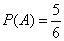
知识点
非空数集



①




正确答案
解析
略
知识点
某校为“市高中数学竞赛”进行选拔性测试,规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰,现有100人参加测试,测试成绩的频率分布直方图如图(4).
(1)求获得参赛资格的人数;
(2)根据频率分布直方图,估算这100名学生
测试的平均成绩;
(3)现在成绩



正确答案
见解析。
解析
(1)由频率分布直方图得,获得参赛资格的人数为:100×(0.0050+0.0045+0.0030)×20=25人。
(2)设100名学生的平均成绩为,则
=[×0.0065+×0.0140+×0.0170+×0.0050+×0.0045+×0.0030]×20=78.4分。
(3) 成绩在




从

其中含有

知识点
某中学高三(1)班有男同学30名,女同学10名,老师按照分层抽样的方法组建了一个
(1)求小组中男、女同学的人数;
(2)从这个小组中先后选出2名同学进行测试,求选出的2名同学中恰有一名女同学的概率。
正确答案
(1)3;1
(2)
解析
(1)设小组中有

所以小组中男、女同学的人数分别为3,1. …………………………………5分
(2)把















所以选出的两名同学中恰有一名女同学的概率为
知识点
盒中装有形状、大小完全相同的7个球,其中红色球4个,黄色球3个,若从中随机取出2个球,则所取出的2个球颜色不同的概率等于 。
正确答案
解析
略
知识点
某网站体育板块足球栏目组发起了“射手的上场时间与进球有关系”的调查活动,在所有参加调查的人中,持“有关系”、“无关系”、“不知道”态度的人数如下表所示:
(1) 在所有参加调查的人中,用分层抽样的方法抽取n个人,已知从持“有关系“态度的人中抽取45人,求n的值;
(2) 在持“不知道”态度的人中,用分层抽样的方法抽取5人,从这5人中任意选取2人,求2人中至少有一人在40岁以下的概率;
(3) 在接受调查的人中,有8人给这项活动打出分数如下:9.4,8.6,9.2,8.7,9.3.,9.0,8.2.把这8个人打出的分数看作一个总体,从中任取一个分数,求该分数与总体平均分之差的绝对值超过0.6的概率。
正确答案
见解析。
解析
知识点
在一个袋子中装有分别标注1,2,3,4,5的五个小球,这些小球除标注的数字外完全相同,现从中随机取出2个小球,则取出小球标注的数字之差的绝对值为2或4的概率是( )
正确答案
解析
这是一个古典概型,只要做出事件总数和满足条件的事件数就可以得到结果,从5个球中任取两个有C52=10种方法,数字之差的绝对值为2或4的有四种结果,根据概率公式得到结果。
解:从5个球中任取两个有C52=10种方法,
数字之差的绝对值为2或4的有(1,3),(2,4),(3,5),(1,5)四种结果,
∴P=

故选C
知识点
一厂家向用户提供的一箱产品共10件,其中有2件次品,用户随机抽取3件产品进行检验,若这3件产品中至少有一件次品,就拒收这箱产品;若这3件产品中没有次品,就接收这箱产品,那么这箱产品被用户拒收的概率是 ,(用数字作答)
正确答案
解析
略
知识点
扫码查看完整答案与解析