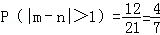- 随机事件及其概率
- 共412题
科学研究表明:一般情况下,在一节40分钟的课中,学生的注意力随教师讲课的时间变化而变化。开始上课时,学生的注意力逐步增强,随后学生的注意力开始分散。经过实验分析,得出学生的注意力指数

(1)如果学生的注意力指数不低于80,称为“理想听课状态”,则在一节40分钟的课中学生处于“理想听课状态”所持续的时间有多长?(精确到1分钟)
(2)现有一道数学压轴题,教师必须持续讲解24分钟,为了使效果更好,要求学生的注意力指数在这24分钟内的最低值达到最大,那么,教师上课后从第几分钟开始讲解这道题?(精确到1分钟)
正确答案
(1)

解析
解析:(1)由于学生的注意力指数不低于80,即
当


当


所以
故学生处于“理想听课状态”所持续的时间有
(2)设教师上课后从第
所以
要学生的注意力指数最低值达到最大,只需
即
解得
所以,教师上课后从第
知识点
某校从高一年级学生中随机抽取40名学生,将他们的期中考
试数学成绩(满分100分,成绩均为不低于40分的整数)分
成六段:


频率分布直方图。
(1)求图中实数
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在

生中随机选取两名学生,求这两名学生的数学成绩之差
的绝对值不大于10的概率。
正确答案
见解析
解析
(1)解:由于图中所有小矩形的面积之和等于1,
所以
解得
(2)解:根据频率分布直方图,成绩不低于60分的频率为
由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为
(3)解:成绩在



成绩在





若从数学成绩在
















如果两名学生的数学成绩都在



记“这两名学生的数学成绩之差的绝对值不大于10”为事件








所以所求概率为
知识点
某年某省有








(1)请估计该次高考成绩在

(2)考生A填报志愿后,得知另外有4名同分数考生也填报了该志愿。若该志愿计划录取2人,并在同分数考生中随机录取,求考生A被该志愿录取的概率。
正确答案
见解析。
解析
(1)由所给的数据估计该年广东省文科考生成绩在
(2)设另外4名考生分别为







知识点
高三(1)班的一个研究性学习小组在网上查知,某珍稀植物种子在一定条件下发芽成功的概率为
(1)第一小组做了5次这种植物种子的发芽实验(每次均种下一粒种子),求他们的实验恰好有3次成功的概率;
(2)若两小组都做4次试验(每次均种下一粒种子),求第二小组比第一小组多成功3次的概率;
正确答案
见解析。
解析
(1)该事件为5次独立重复试验发生3次
∴P=P5(3)
=
(2)
分布列如下:
∴ E
知识点
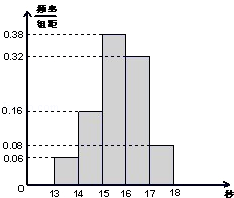
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组;第一组[13,14),第二组[14,15),…,第五组[17,18],下图是按上述分组方法得到的频率分布直方图。
(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两位同学的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m﹣n|>1”的概率。
正确答案
见解析。
解析
(1)由直方图知,成绩在[14,16)内的人数为:50×0.16+50×0.38=27(人),
所以该班成绩良好的人数为27人、
(2)由直方图知,成绩在[13,14)的人数为50×0.06=3人,
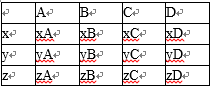
设为为x,y,z;成绩在[17,18]的人数为50×0,08=4人,设为A、B、C、D。
若m,n∈[13,14)时,有xy,xz,yz共3种情况;
若m,n∈[17,18]时,有AB,AC,AD,BC,BD,CD,共6种情况;
若m,n分别在[13,14)和[17,18]内时,
有12种情况、
所以,基本事件总数为3+6+12=21种,事件“|m﹣n|>1”所包含的基本事件个数有12种、
∴
知识点
为了对某课题进行研究,用分层抽样的方法从三所高校
(1)求
(2)若从高校

正确答案
(1)
(2)C的概率
解析
(1)∵
∴
∴
(2)高校


高校



从中选出2人作专题发言,从中选出2人,共有10种选法,即










其中2人都来自高校
故这2人都来自高校C的概率
知识点
若



正确答案
解析
略
知识点
课题组进行城市空气质量调查,按地域把24个城市分成甲、乙、丙三组,对应的城市数分别为4,12,8,若用分层抽样抽取6个城市,则丙组中应抽取的城市数为 。
正确答案
2
解析
解:∵某城市有甲、乙、丙三组,对应的城市数分别为4,12,8。
本市共有城市数24,
∵用分层抽样的方法从中抽取一个容量为6的样本
∴每个个体被抽到的概率是 
∵丙组中对应的城市数8,
∴则丙组中应抽取的城市数为
故答案为2。
知识点
某校从高一年级学生中随机抽取40名学生,将他们的期中考
试数学成绩(满分100分,成绩均为不低于40分的整数)分
成六段:


频率分布直方图。
(1)求图中实数
(2)若该校高一年级共有学生640人,试估计该校高一年级
期中考试数学成绩不低于60分的人数;
(3)若从数学成绩在

生中随机选取两名学生,求这两名学生的数学成绩之差
的绝对值不大于10的概率。
正确答案
见解析
解析
(1)解:由于图中所有小矩形的面积之和等于1,
所以
解得
(2)解:根据频率分布直方图,成绩不低于60分的频率为
由于该校高一年级共有学生640人,利用样本估计总体的思想,可估计该校高一年级数学成绩不低于60分的人数约为
(3)解:成绩在



成绩在





若从数学成绩在
















如果两名学生的数学成绩都在



记“这两名学生的数学成绩之差的绝对值不大于10”为事件








所以所求概率为
知识点
某校一个甲类班x名学生在2011年某次数学测试中,成绩全部介于90分与140分之间,将测试结果按如下方式分成五组,第一组


(1)求x及分布表中m,n,t的值;
(2)设a,b是从第一组或第五组中任意抽取的两名学生的数学测试成绩,求事件“
正确答案
见解析。
解析
(1)
(2)第一组
第五组
则

记“



∴
∴事件“

知识点
扫码查看完整答案与解析