- 随机事件及其概率
- 共412题
豌豆的高矮性状的遗传由其一对基因决定,其中决定高的基因记为D,决定矮的基因记为d,
则杂交所得第一子代的一对基因为Dd,若第二子代的D,d的基因遗传是等可能的(只要有基
因D则其就是高茎,只有两个基因全是d时,才显示矮茎),则第二子代为高茎的概率为 ▲ 。
正确答案
解析
第二子代的一对基因的所有等可能情形为DD,Dd,dD,dd,其中高茎的有DD,Dd,dD共3种,则所求概率为
知识点
某县为增强市民的环境保护意识,面向全县征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组




(1)分别求第3,4,5组的频率.
(2)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?
(3)在(2)的条件下,该县决定在这6名志愿者中随机抽取2名志愿者介绍宣传
经验,求第4组至少有一名志愿者被抽中的概率.
正确答案
见解析。
解析
(1) 由题设可知,第3组的频率为0.06×5=0.3,
第4组的频率为0.04×5=0.2,
第5组的频率为0.
(2)第3组的人数为0.3×
第4组的人数为0.2×100=20,
第5组的人数为0.1×100=10.
因为第3,4,5组共有60名志愿者,所以利用分层抽样的方法在60名志愿者中抽取6名志愿者,每组抽取的人数分别为:
第3组:


所以应从第3,4,5组中分别抽取3人,2
(3)记第3组的3名志愿者为A1,A2,A3,第4组的2名志愿者为B1,B2,第5组的1名志愿者为C1.
则从6名志愿者中抽取2名志愿者有:
(A1,A2), (A1,A3),(A1,B1),(A1,B2),(A1,C1),(A2,A3),(A2,B1),(A2,B2),(A2,C1),(A3,B1),(A3,B2),
(A3,C1),(B1,B2),(B1,C1),(B2,C1),共有15种.
其中第4组的2名志愿者B1,B2至少有一名志愿者被抽中的有:
(A1,B1), (A1,B2), (A2,B1), (A2,B2), (A3,B1), (A3,B2), (B1,B2), (B1,C1), (B2,C1
所以第4组至少有一名志愿者被抽中的概率为
知识点
继“三鹿奶粉”,“瘦肉精”, “地沟油”等事件的发生之后,食品安全问题屡屡发生,引起了国务院的高度重视.为了加强食品的安全,某食品安检部门调查一个海水养殖场的养殖鱼的有关情况,安检人员从这个海水养殖场中不同位置共捕捞出100条鱼,称得每条鱼的重量(单位:kg),并将所得数据进行统计得下表.若规定超过正常生长的速度为1.0~1.2kg/年的比重超过15%,则认为所饲养的鱼有问题,否则认为所饲养的鱼没有问题。
(1)根据数据统计表,估计数据落在[1.20,1.30)中的概率约为多少,并判断此养殖场所饲养的鱼是否存在问题?
(2)上面捕捞的100条鱼中间,从重量在



正确答案
见解析。
解析
(1)捕捞的100条鱼中间,数据落在

数据落在

所以数据落在[1.20,1.30)中的概率约为
由于


故饲养的这批鱼没有问题. (6分)
(2)重量在
重量在


而恰好所取得鱼重量在


所以恰好所取得鱼重量在


知识点
在集合
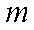




正确答案
解析
由题意得到的
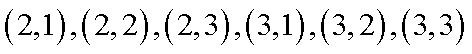


知识点
某校为了解学生的睡觉情况,随机调查了50名学生,得到他们在某一天各自的睡眠时间的数据,结果用下面的条形图表示,根据条形图可得这50名学生这一天平均每人的睡眠时间为_______________
正确答案

解析

知识点
已知数字发生器每次等可能地输出数字1或2中的一个数字,则连续输出的4个数字之和能被3整除的概率是 。
正确答案
解析
由题意知本题是一个古典概型,
∵ 试验发生包含的事件是连续输出的4个数字,
每次等可能地输出数字1或2中的一个数字,
则有2×2×2×2=16,共有16种结果,
满足条件的事件是连续输出的4个数字之和能被3整除,即连续输出的4个数字中有两个1和两个2,表示为1,1,2,2;1,2,1,2;1,2,2,1;2,1,1,2;2,2,1,1;2,1,2,1。
可知有6种结果,
∴ 根据古典概型概率公式得到P=

故答案为:
知识点
在一本书中,分组统计100个句子中的字数,得出下列结果:字数1~5个的5句,字数6~10个的27句,字数11~15个的32句,字数16~20个的21句,字数21~25个的9句,字数26~30
个的6句,利用组中值可估计该书中平均每个句子所包含的字数为 ▲ 。
正确答案
14
解析
利用组中值得平均每个句子所包含的字数为
知识点
为了分析某篮球运动员在比赛中发挥的稳定程度,统计了该运动员在6场比赛中的得分,用茎叶图表示如图所示,则该组数据的方差为 .
正确答案
5
解析
平均数
故方差
知识点
若在区间





正确答案
解析
由题意知
直线


∴阴影梯形的面积为
而区间


知识点
在数轴上区间


正确答案
解析



知识点
扫码查看完整答案与解析

















