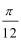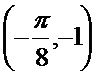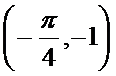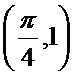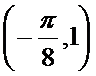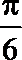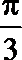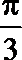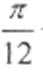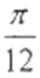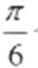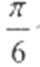- 函数y=Asin(ωx+φ)的图象变换
- 共79题
7.已知函数





正确答案
解析
解析已在路上飞奔,马上就到!
知识点
10.已知



正确答案
解析
解析已在路上飞奔,马上就到!
知识点
6.把函数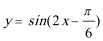
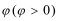
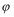
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知向量


(1)求函数
(2)当

(3)说明

正确答案
(2)由
解得
∵取k=0和1且


∴


法二:∵

∴由

解得

∴


(3)



再把所得各点的横坐标缩短到原来的
最后把所得各点的纵坐标伸长为原来的2倍(横坐标不变),
得到
解析
解析已在路上飞奔,马上就到!
知识点
7.设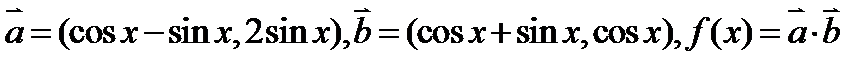
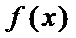
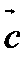
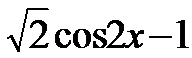
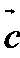
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.要得到函数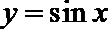
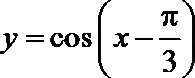
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.要得到函数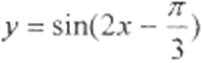

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
9.要得到函数

正确答案
解析
因为



知识点
8.设函数




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知函数



(1)若
(2)若


正确答案
(1)
=
f(C)=
因为

由余弦定理知:
因
b=3a
解得:a=1,b=3
(2)由条件知
所以
所以
因为
所以


于是
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析