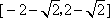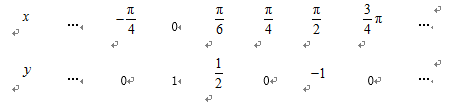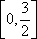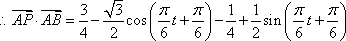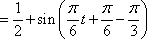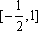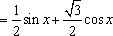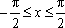- 由y=Asin(ωx+φ)的部分图象确定其解析式
- 共50题
已知函数
(1)求函数f(x)的表达式;
(2)若

正确答案
见解析。
解析
16.解:(1)依题意,







(2)



知识点
将函数





正确答案
解析
本题考查的三角函数的图像的平移,把






知识点
设函数f(x)=sin2ωx+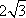

(1)求函数f(x)的最小正周期;
(2)若y=f(x)的图象经过点(
正确答案
(1) 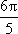
解析
(1)因为f(x)=sin2ωx-cos2ωx+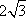
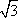
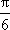
由直线x=π是y=f(x)图象的一条对称轴,可得sin(2ωπ-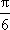
所以2ωπ-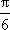
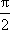
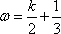
又ω∈(
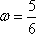
所以f(x)的最小正周期是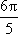
(2)由y=f(x)的图象过点(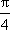
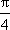
即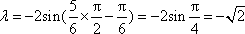
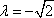
故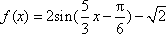
知识点
已知函数
(1)求函数f(x)的解析式,并写出f(x)的单调减区间;
(2)△ABC的内角分别是A,B,C,若f(A)=1,cosB=
正确答案
见解析。
解析
(1)由图象最高点得A=1,
由周期
当


因为


由图象可得

(2)由(1)可知, 






知识点
已知函数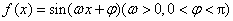
(1)求
(2)若在△ABC中,AC=2,BC=3,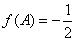
正确答案
见解析。
解析
知识点
同时具有性质:“①最小正周期是



正确答案
解析
略
知识点
函数

正确答案
解析
略
知识点
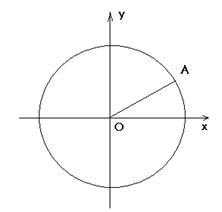
如图,设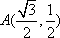


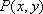
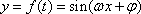
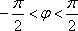
(1)求点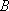
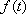
(2)若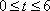
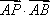
正确答案
(1)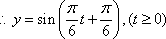
解析
(1)当

所以
所以,点B的坐标是(0,1)
又
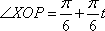
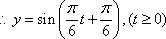
(2)由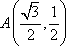
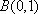
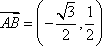
又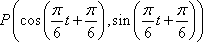
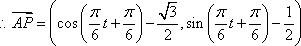
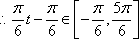
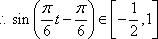
所以,

知识点
已知函数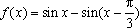
(1)求
(2)求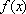

正确答案
(1)1
(2)
解析
(1)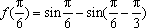
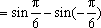
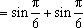
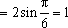
(2)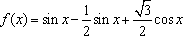
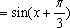
因为
所以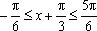
所以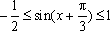
所以
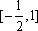
知识点
函数

正确答案
解析
略
知识点
扫码查看完整答案与解析