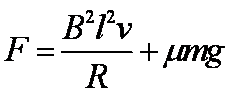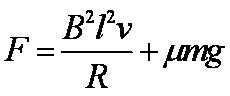- 感生电动势、动生电动势
- 共108题
如图1所示,矩形导线框ABCD固定在匀强磁场中,磁感线垂直于线框所在平面向里。规定垂直于线框所在平面向里为磁场的正方向;线框中沿着ABCDA方向为感应电流i的正方向。要在线框中产生如图2所示的感应电流,则磁感应强度B随时间t变化的规律可能为
正确答案
解析
略
知识点
如图10所示, 金属棒a从高为h处自静止起沿光滑的弧形导轨下滑,进入光滑导轨的水平部分,导轨的水平部分处于竖直向下的匀强磁场中,在水平部分原先静止有另一根金属棒b,两根棒的质量关系是ma=2mb=2m,整个水平导轨足够长并处于广阔的匀强磁场中。
⑴当金属棒a刚进入磁场的瞬间,两棒的加速度大小之比是多少?
⑵设两金属棒的总电阻为R,当金属棒a刚进入磁场的瞬间,回路中的感应电流是多大?
⑶假设金属棒a始终没跟金属棒b相碰,则两棒的最终速度各多大?
⑷上述整个过程中两根金属棒和导轨所组成的回路中消耗的电能是多少?
正确答案
见解析。
解析
⑴因为两棒所受安培力大小相等方向相反,由牛顿第二定律可得


⑵a从高h处下滑到底端时的速度设为v0
由机械能守恒得:

棒a产生感应电动势为E=BLv0=BL

⑶a做加速运动,b做减速运动,直到两棒的速度相同,回路中感应电流为零,两棒的运动达到稳定,设此时的速度为v,在水平轨道,安培力大小相等,方向相反,所以系统动量守恒。


⑷设回路消耗的总的电能为W,由能量守恒得


知识点
如图所示,竖直平面内有足够长、不计电阻的两组平行光滑金属导轨,宽度均为L=0.5m,上方连接一个阻值R=1Ω的定值电阻,虚线下方的区域内存在垂直纸面向里的磁感应强度B=2T的匀强磁场。完全相同的两根金属杆1和2靠在导轨上,金属杆长与导轨等宽且与导轨接触良好,电阻均为r =0.5Ω。将金属杆1固定在磁场的上边缘(仍在此磁场内),金属杆2从磁场边界上方h0=0.8m处由静止释放,进入磁场后恰作匀速运动。(g取10m/s2)求:
(1)金属杆的质量m;
(2)若金属杆2从磁场边界上方h1=0.2m处由静止释放,进入磁场下落一段距离后做匀速运动。在金属杆2加速的过程中整个回路产生了1.4J的电热。求此过程中流过电阻R的电荷量q;
(3)若金属杆2仍然从磁场边界上方h1=0.2m处由静止释放,在金属杆2进入磁场的同时释放金属杆1,试求两根金属杆各自的最大速度。
正确答案
见解析。
解析
(1)金属杆2进入磁场前做自由落体运动,进入磁场的速度
vm=

金属杆2进入磁场后切割磁感线,回路中产生感应电流,有
感应电动势E=BLvm,感应电流
金属杆恰做匀速运动,受安培力和重力平衡:mg=BIL
解出m=

(2)金属杆2自由下落h1,进入磁场,做加速运动,设金属杆2在磁场内下降h2后达到匀速运动,在加速的过程中,部分机械能转化为电能产生电热,有
mg(h1+h2)=
可得 h2=
金属杆2进入磁场到匀速运动的过程中

解出流过电阻的电量 q=

(3)金属杆2刚进入磁场时的速度v=

金属杆2进入磁场同时释放金属杆1后,回路中有感应电流,两杆都受安培力和重力,且受力情况相同,都向下做加速运动,随速度增大,感应电流增大,安培力增大,直到安培力和重力相等时,速度达到最大。
金属杆1和2产生的感应电动势为E1=BLv1,E2=BLv2
感应电流为
达到最大速度时杆的重力等于安培力
mg=BIL
整理得到:v1+ v2=
代入数据得v1+ v2=4 m/s……………… ①
因为两个金属杆任何时刻受力情况相同,因此任何时刻两者的加速度也都相同,在相同时间内速度的增量也必相同,即:v1-0 =v2- v
代入数据得v2= v1+2……………………………………………………… ②
① ②两式联立求出:v1=1m/s,v2=3m/s
知识点
如图所示,边长为


正确答案
解析
略
知识点
4.题4图为无线充电技术中使用的受电线圈示意图,线圈匝数为






正确答案
解析
解析已在路上飞奔,马上就到!
知识点
2.如图,空间有一匀强磁场,一直金属棒与磁感应强度方向垂直,当它以速度v沿与棒和磁感应强度都垂直的方向运动时,棒两端的感应电动势大小ε,将此棒弯成两段长度相等且相互垂直的折弯,置于磁感应强度相垂直的平面内,当它沿两段折线夹角平分线的方向以速度v运动时,棒两端的感应电动势大小为

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19.如图所示,abcd为水平放置的平行“
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
35.如图17(a)所示,平行长直金属导轨
(1)棒进入磁场前,回路中的电动势E;
(2)棒在运动过程中受到的最大安培力F,以及棒通过三角形abd区域时电流i与时间t的关系式。
正确答案
(1)E=0.04V;
(2)Fm=0.04N,i=t-1(其中,1s≤t≤1.2s)。
解析
解析已在路上飞奔,马上就到!
知识点
13.如图,两平行金属导轨位于同一水平面上,相距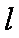
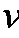
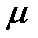
(1)电阻R消耗的功率;
(2)水平外力的大小。
正确答案
(1)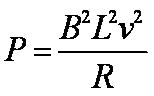
试题解析:(1)导体切割磁感线运动产生的电动势为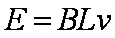
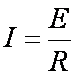
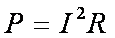
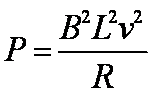
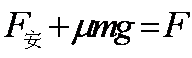
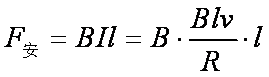
解析
解析已在路上飞奔,马上就到!
知识点
22. 如图所示,足够长的平行光滑金属导轨水平放置,宽度 L = 0.4 m,一端连接R=1 Ω的电阻,导轨所在的空间存在竖直向下的匀强磁场,磁感应强度 B = 1 T,导体棒 MN 放在导轨上,其长度恰好等于导轨间距,与导轨接触良好。导轨和导体棒的电阻均可忽略不计。在平行于导轨的拉力 F 作用下,导体棒沿导轨向右匀速运动,速度 v = 5 m/s ,求:
( 1 ) 感应电动势 E 和感应电流 I ;
( 2 ) 在 0.1 s 时间内,拉力的冲量 的大小;
( 3 ) 若将 MN 换为电阻为 r = 1 Ω的 导体棒,其它条件不变,求导体棒两端的电压 U。
正确答案
(1)根据动生电动势公式得E=BLv = 1T ×0.4m ×5m /s =2V
故感应电流
(2)金属棒在匀速运动过程中,所受的安培力大小为
F安= BIL =0.8N, 因为是匀速直线运动,所以导体棒所受拉力F = F安 = 0.8N
所以拉力的冲量 IF =F t=0.8 N× 0.1 s=0.08 N
(3)导体棒两端电压
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析