1
题型:简答题
|
21.已知向量a、b、c是同一平面内的三个向量,其中a=(1,2).
(1)若|c|=2
(2)若|b|=
正确答案
(1)令c=(x,y),则由|c|=2


又由a∥c知,2x-y=0②
联立①②可解得:

故c=(2,4)或c=(-2,-4).
(2)由a+2b与2a-b垂直知(a+2b)·(2a-b)=0,
即2a2+3a·b-2b2=0,∴a·b=
即|a||b|cosθ=

而由a=(1,2)知|a|=

∵θ∈[0,π],∴θ=π.
解析
解析已在路上飞奔,马上就到!
知识点
向量的模平行向量与共线向量平面向量数量积的运算数量积表示两个向量的夹角数量积判断两个平面向量的垂直关系
1
题型:填空题
|
13.已知平面向量





正确答案
解析
分三种情况考虑:
(1)


(1)


(1)


三者比较大小后知应选
知识点
集合的相等向量的模平面向量数量积的运算
1
题型:填空题
|
14.已知向量a=(1,

正确答案
2
解析
根据a=(1,

所以
即
考查方向
本题主要考查了平面向量的坐标运算,数量积的概念表示,向量的模的求解。
解题思路
本题考查平面向量的有关问题,
解题步骤如下:根据向量的坐标表示写出

易错点
1、向量模的求解出错;
2、向量的数量积的定义理解出错。
知识点
向量的模平面向量数量积的运算数量积表示两个向量的夹角
1
题型:
单选题
|
4.设


正确答案
C
解析



所以
考查方向
本题主要考察充分必要条件的判断、向量的基本运算以及向量的平行的性质,难度中等,是高考热点之一。充分必要条件的判断在高考中常结合立体几何、三角函数等各章节的基本知识出题。
解题思路
由基本运算入手
易错点
考虑过多,想到向量的零向量,以及向量平行的同向和反向两种情况而误导出错
知识点
充要条件的判定向量的模平行向量与共线向量
1
题型:
单选题
|
4.设向量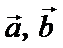
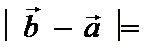
正确答案
A
解析

考查方向
本题主要考查平面向量的点积
解题思路
先使用向量减法的几何意义做
易错点
没理解向量模的 意义
知识点
向量的模平面向量数量积的运算
下一知识点 : 零向量
扫码查看完整答案与解析