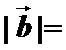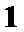8．已知
A
B
C
D
正确答案
解析
考查方向
解题思路
先根据垂直数量积为零求出未知参数m，再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式。
知识点
4．已知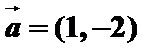
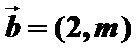
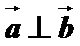
A
B
C
D
正确答案
解析
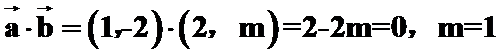
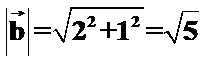
考查方向
解题思路
先根据垂直数量积为零求出未知参数m，再计算出b向量的模。
易错点
本题不知道向量垂直坐标满足的关系式 。
知识点
5. 已知不共线的两个向量
A
B2
C
D4
正确答案
解析
将已知的2个式子左右同时平方再相减即可得
【修改点】将已知
考查方向
解题思路
由垂直数量积为0得一个式子，由已知的模左右同时平方得一个式子，两式联立即可解出。
易错点
模的计算方法不清楚。
知识点
12．对
A
B
C
D
正确答案
解析
考查方向
解题思路
1）由向量可知
2）向量转化问题变为圆的方程
长度不超过6等价于
3）问题转化为两圆内切或内涵，进而求出n的范围
4）根据几何概型得出结果
易错点
主要易错于几何意义的构建
知识点
13.已知
正确答案
解析
试题分析：根据向量数量积的定义求出向量的夹角，再利用题中给出的条件求出
∵
故答案为：
考查方向
解题思路
根据数量积得出
易错点
向量数量积的公式的应用.
知识点
7．已知非零向量
A
B
C
D
正确答案
解析
由已知可得
考查方向
解题思路
本题考查向量的数量积运算与向量夹角之间的关系，采用两向量垂直时其数量积为零来进行转化.本题属于基础题.
易错点
注意运算的准确性
知识点
依据《注册安全工程师管理规定》，注册安全工程师实行分类注册，注册类别包括 ( )。
A．煤矿安全
B．非煤矿矿山安全
C．建筑施工安全
D．危险物品安全
E．烟花爆竹安全
正确答案
A,B,C,D
解析
暂无解析
A公司欠债权人甲200万元，后A公司分立为A、B两个公司，A、B两公司在分立时就对甲的债务达成协议：由A公司承担150万元，B公司承担50万元。但该协议并没有告知债权人甲。则此时200万元的债务由谁承担( )。
A．按照A和B协议的方式承担
B．由A公司承担
C．由A、B两公司各承担100万元
D．由A、B两公司承担连带责任
正确答案
D
解析
暂无解析
3.平面向量
A
B0
C
D2
正确答案
解析
由
考查方向
本题主要考查了向量数量积的定义及数量积运算性质，在近几年的各省高考题出现的频率较高。
易错点
求模时忘记开方导致出错。
知识点
13．向量
正确答案
解析
由
考查方向
本题主要考查向量的相关知识。
解题思路
将垂直条件转化为数量积为0，代入数据求出
易错点
1.不能将垂直的条件进行转化。
2.夹角公式不清楚
知识点
扫码查看完整答案与解析