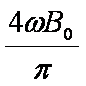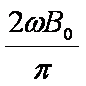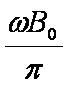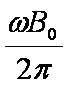- 法拉第电磁感应定律
- 共387题
如图所示,一对光滑的平行金属导轨固定在同一水平面内,导轨间距l=0.5 m,左端接有阻值R=0.3 Ω的电阻,一质量m=0.1 kg,电阻r=0.1 Ω的金属棒MN放置在导轨上,整个装置置于竖直向上的匀强磁场中,磁场的磁感应强度B=0.4 T,棒在水平向右的外力作用下,由静止开始以a=2 m/s2的加速度做匀加速运动,当棒的位移x=9 m时撤去外力,棒继续运动一段距离后停下来,已知撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1,导轨足够长且电阻不计,棒在运动过程中始终与导轨垂直且两端与导轨保持良好接触,求
(1)棒在匀加速运动过程中,通过电阻R的电荷量q;
(2)撤去外力后回路中产生的焦耳热Q2;
(3)外力做的功WF。
正确答案
(1)4.5 C
(2)1.8 J
(3)5.4 J
解析
(1)设棒匀加速运动的时间为



其中
设回路中的平均电流为

则通过电阻R的电荷量为
联立①②③④式,代入数据得q=4.5 C⑤
(2)设撤去外力时棒的速度为v,对棒的匀加速运动过程,由运动学公式得v2=2ax⑥
设棒在撤去外力后的运动过程中安培力做功为W,由动能定理得W=0-
撤去外力后回路中产生的焦耳热
Q2=-W⑧
联立⑥⑦⑧式,代入数据得
Q2=1.8 J⑨
(3)由题意知,撤去外力前后回路中产生的焦耳热之比Q1∶Q2=2∶1,可得Q1=3.6 J⑩
在棒运动的整个过程中,由功能关系可知WF=Q1+Q2⑪
由⑨⑩⑪式得WF=5.4 J。
知识点
如图所示,正方形区域MNPQ内有垂直纸面向里的匀强磁场,在外力作用下,一正方形闭合刚性导线框沿QN方向匀速运动,t=0时刻,其四个顶点M′、N′、P′、Q′恰好在磁场边界中点,下列图象中能反映线框所受安培力f的大小随时间t变化规律的是( )
正确答案
解析
第一段时间从初位置到M′N′离开磁场,图甲表示该过程的任意一个位置,切割磁感线的有效长度为M1A与N1B之和,即为M1M′长度的2倍,此时电动势E=2Bvtv,线框受的安培力

知识点
如图,两根足够长的金属导轨ab、cd竖直放置,导轨间距离为L,电阻不计。在导轨上端并接两个额定功率均为P、电阻均为R的小灯泡。整个系统置于匀强磁场中,磁感应强度方向与导轨所在平面垂直。现将一质量为m、电阻可以忽略的金属棒MN从图示位置由静止开始释放。金属棒下落过程中保持水平,
(1)磁感应强度的大小;
(2)灯泡正常发光时导体棒的运动速率。
正确答案
(1)设小灯泡的额定电流I0,有:P=I02R①
由题意,在金属棒沿着导轨竖直下落的某时刻后,小灯泡保持正常发光,流经MN的电流为 I=2I0②
此时刻金属棒MN所受的重力和安培力相等,下落的速度达到最大值,有 mg=BLI③
联立①②③式得 
(2)设灯泡正常发光时,导体棒的速率为v,由电磁感应定律与欧姆定律得
E=BLv⑤
E=RI0⑥
联立①②④⑤⑥式得 v=
解析
略。
知识点
如图甲,一圆形闭合铜环由高处从静止开始下落,穿过一根竖直悬挂的条形磁铁,铜环的中心轴线与条形磁铁的中轴始终保持重合。若取磁铁中心O为坐标原点,建立竖直向下正方向的x轴,则图乙中最能正确反映环中感应电流i随环心位置坐标x变化的关系图像是
正确答案
解析
由楞次定律可知,感应线圈中电流方向变化,综合分析两个峰值不可能相等,由排除法可知正确答案选D
知识点
如图,一载流长直导线和一矩形导线框固定在同一平面内,线框在长直导线右侧,且其长边与长直导线平行。已知在t=0到t=t1的时间间隔内,直导线中电流i发生某种变化,而线框中感应电流总是沿顺时针方向;线框受到的安培力的合力先水平向左、后水平向右。设电流i正方向与图中箭头方向相同,则i随时间t变化的图线可能是
正确答案
解析
要求框中感应电流顺时针,根据楞次定律,可知框内磁场要么向里减弱(载流直导线中电流正向减小),要么向外增强(载流直导线中电流负向增大)。线框受安培力向左时,载流直导线电流一定在减小,线框受安培力向右时,载流直导线中电流一定在增大。故答案选A。
知识点
如图所示,质量

















(1)求框架开始运动时
(2)从



正确答案
(1)6m/s (2)1.1m
解析
(1)ab对框架的压力 
框架受水平面的支持力
依题意,最大静摩擦力等于滑动摩擦力,则框架受到最大静摩擦力

ab中的感应电动势E=
MN中电流 
MN受到的安培力 
框架开始运动时
由上述各式代入数据解得v=6m/s⑧
(2)闭合回路中产生的总热量: 
由能量守恒定律,得:
代入数据解得x=1.1m⑾
知识点
如图,均匀磁场中有一由半圆弧及其直径构成的导线框,半圆直径与磁场边缘重合;磁场方向垂直于半圆面(纸面)向里,磁感应强度大小为B0.使该线框从静止开始绕过圆心O、垂直于半圆面的轴以角速度ω匀速转动半周,在线框中产生感应电流。现使线框保持图中所示位置,磁感应强度大小随时间线性变化。为了产生与线框转动半周过程中同样大小的电流,磁感应强度随时间的变化率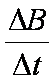
正确答案
解析
匀速转动时感应电动势与磁场变化时感应电动势相同即可。匀速转动时感应电动势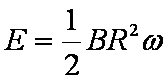
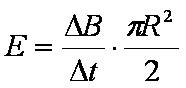
知识点
一矩形线框置于匀强磁场中,线框平面与磁场方向垂直,先保持线框的面积不变,将磁感应强度在1 s 时间内均匀地增大到原来的两倍,接着保持增大后的磁感应强度不变,在1 s 时间内,再将线框的面积均匀地减小到原来的一半,先后两个过程中,线框中感应电动势的比值为
正确答案
解析
本题考查感应电动势的计算。


知识点
如图所示,两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上,导轨上端连接一个定值电阻。导体棒a和b放在导轨上,与导轨垂直开良好接触。斜面上水平虚线PQ以下区域内,存在着垂直穿过斜面向上的匀强磁场。现对a棒施以平行导轨斜向上的拉力,使它沿导轨匀速向上运动,此时放在导轨下端的b棒恰好静止。当a棒运动到磁场的上边界PQ处时,撤去拉力,a棒将继续沿导轨向上运动一小段距离后再向下滑动,此时b棒已滑离导轨。当a棒再次滑回到磁场上边界PQ处时,又恰能沿导轨匀速向下运动。已知a棒、b棒和定值电阻的阻值均为R,b棒的质量为m,重力加速度为g,导轨电阻不计。求
(1)a棒在磁场中沿导轨向上运动的过程中,a棒中的电流强度Ia与定值电阻中的电流强度Ic之比;
(2)a棒质量ma;
(3)a棒在磁场中沿导轨向上运动时所受的拉力F。
正确答案
见解析
解析
(1)






解得:
(2)由于







当


向上匀速运动时,



由以上各式联立解得:
(3)由题可知导体棒

知识点
如图,均匀带正电的绝缘圆环a与金属圆环b同心共面放置,当a绕O点在其所在平面内旋转时,b中产生顺时针方向的感应电流,且具有收缩趋势,由此可知,圆环a
正确答案
解析
由题意知:圆环a b电流方向相同,在安培力作用下体现出相互吸引的效果,且根据楞次定律“增反减同”原则,a环在减速旋转。
知识点
扫码查看完整答案与解析