- 虚数单位i及其性质
- 共304题
16.观察下列等式:
(1)若




(2)若




依据你发现的规律,若

正确答案
解析
由(1)可知模长为1的复数的任何次方的模还是1,由(2)可知任何复数都可以化为一个非负实数乘以一个对应的模长为1的复数,结合(1)(2),
可知
知识点
(x2+
正确答案
解析
∵(x2+

展开式的通项为Tr+1=


令8﹣2r=0,解得r=4;
∴常数项T5=
∴a4=4,
又a>0,
∴a=
故答案为:
知识点
13.(
正确答案
6
解析
设第
知识点
1.若复数z满足zi=1-i,则z等于()
正确答案
解析
∵
知识点
已知曲线C1的参数方程为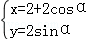
标原点为极点,x轴的非负半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρcos(θ+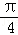
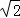
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)。
正确答案
见解析。
解析
(1)利用cos2α+sin2α=1将曲线C1的参数方程消去参数α,即可得出C1的普通方程,将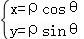
(2)由曲线C2的极坐标方程ρcos(θ+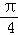
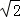
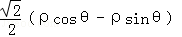
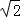
(1)将曲线C1的参数方程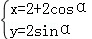
∴C1的普通方程为:x2+y2﹣4x=0。
将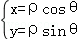
∴C1的极坐标方程为ρ=4cosθ。
(2)由曲线C2的极坐标方程ρcos(θ+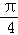
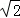
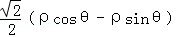
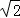
由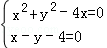
解得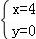
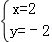
∴C1与C2交点的直角坐标分别为(4,0),(2,﹣2)。
可得极坐标分别为(4,0)或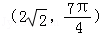
知识点
扫码查看完整答案与解析




