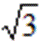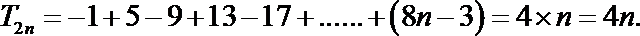- 数列
- 共2062题
16.整数数列{



正确答案
987
解析
解析已在路上飞奔,马上就到!
知识点
19.正项等比数列{an}中,
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:
正确答案
(1)
(2)
解析
解析已在路上飞奔,马上就到!
知识点
17.数列








正确答案

解析
解析已在路上飞奔,马上就到!
知识点
12. 若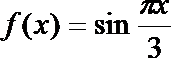
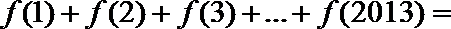
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.数列



正确答案
420
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
19.已知数列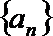
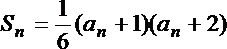
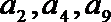
(1)求数列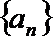
(2)设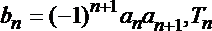

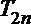
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
23.设数列





(1)若

(2)若

(3)若


正确答案
(1)由题意,得
解
∴

(2)由题意,得
对于正整数,由

根据
当

当

∴

(3)假设存在p和q满足条件,由不等式


∵


即
当



这与上述结论矛盾!
当



∴ 存在p和q,使得
p和q的取值范围分别是
解析
解析已在路上飞奔,马上就到!
知识点
17.阅读程序框图(图中n∈N*),回答下面的问题。
(Ⅰ)当n=3时,求S的值;
(Ⅱ)当S<100时,求n的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
17.已知数列


(Ⅰ)数列
(Ⅱ)数列

正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14.已知数列

正确答案
解析
当n=1时,a1=S1=9;
当n≥2时,an=Sn-Sn-1=11-2n,由于n=1时,a1=9也满足11-2n,因此an=11-2n.
(1)当n>5时,Tn=|a1|+|a2|+…+|an|=-Sn+2S5=n2-10n+50,
(2)当n≤5时,Tn=|a1|+|a2|+…+|an|=-(a1+a2+…+an)=10n-n2,
综合(1)(2),得Tn=
知识点
7. 数列{an}的通项公式an=ncos,其前n项和为Sn,则S2016等于( )
正确答案
解析
其中所有的奇数项都为0,而偶数项是分别为第二项是-2,第四项是4,第六项是-6,第八项是8,这样可以将每2项相加放在一起,刚好有1008个偶数项,即可以组成504组,每组的值为2,所有答案就为1008,故A正确。
考查方向
解题思路
算出前4项并找到这个数列的规律,最后用求和公式解决。
易错点
1、不能找到数列的周期性,没有找到规律导致无法计算下去。
知识点
17.已知等差数列{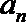
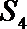
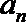
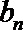
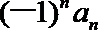
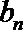
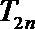
正确答案
an=4n-3; T2n=4n
解析
⑴由已知条件: 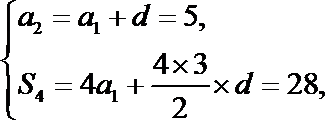
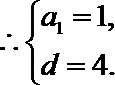
⑵由⑴可得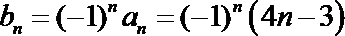
考查方向
本题主要考查数列的综合运算
易错点
本题易在求和时发生错误。
知识点
11. 已知函数


正确答案
解析


所以答案为50,选择A
考查方向
解题思路
先求出通项公式an,然后两项一组,即可求解数列的钱50项和
易错点
通项公式不会求
知识点
16.数列{an}的前n项和为Sn,若Sn-Sn一1=2n-l (
正确答案
5
解析
由条件Sn-Sn一1=2n-l (
当n=3时,S3-S2=2×3-1=5,即a3=5
所以a1+a3=5
考查方向
解题思路
本题考查数列递推式,解题步骤如下:
根据条件求出S1= a1=0;2. 再根据S3-S2=a3求出a3.即可得到答案
易错点
对递推式不熟悉,代入的时候出错。
知识点
扫码查看完整答案与解析