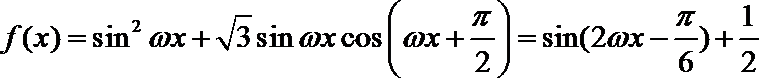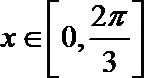- 正弦函数的定义域和值域
- 共124题
1
题型:简答题
|
23. (本题满分18分)本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
若无穷数列




(1)若




(2)若无穷数列






(3)设




正确答案
知识点
正弦函数的定义域和值域
1
题型:简答题
|
在

15.求
16.求
第(1)小题正确答案及相关解析
正确答案
(1)
解析
(1)根据余弦定理公式求出cosB的值,进而根据B的取值范围求B的大小;
考查方向
1.三角恒等变形;2.余弦定理.
解题思路
正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想.
易错点
1)正余弦定理,
2)三角恒等变形公式
第(2)小题正确答案及相关解析
正确答案
(2)
解析
考查方向
1.三角恒等变形;2.余弦定理.
解题思路
正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想.
易错点
1)正余弦定理,
2)三角恒等变形公式
1
题型:填空题
|
7、方程

正确答案
解析
知识点
正弦函数的定义域和值域
1
题型:
单选题
|
6.已知


正确答案
A
知识点
正弦函数的定义域和值域
1
题型:
单选题
|
4.已知函数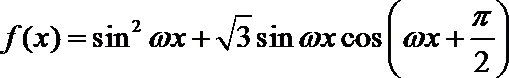
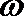

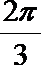
正确答案
A
解析
∵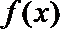
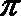
∴
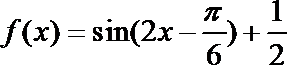
∵
∴

所以答案选A
考查方向
本题主要考查了三角函数的周期和值域
解题思路
利用利用辅助角公式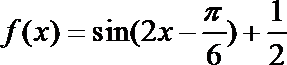
易错点
利用辅助角公式化简函数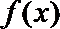
知识点
三角函数的周期性及其求法正弦函数的定义域和值域三角函数中的恒等变换应用
下一知识点 : 正弦函数的单调性
扫码查看完整答案与解析