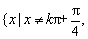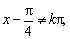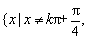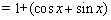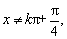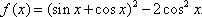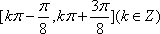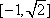- 正弦函数的定义域和值域
- 共124题
已知函数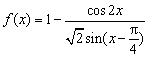
(1)求函数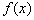
(2) 求函数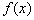
正确答案
(1)
(2) 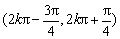
解析
(1)因为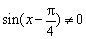
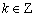
所以函数的定义域为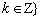
(2)因为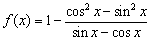
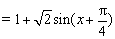
又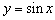
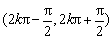
令 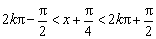
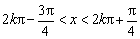
又注意到
所以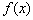
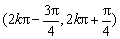
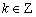
知识点
已知函数
(1)求函数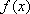
(2)求函数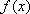
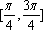
正确答案
(1)最小正周期T=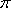
(2)
解析
(1)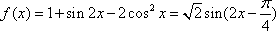

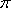
单调增区间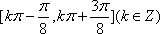
(2)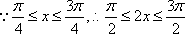
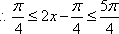
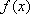
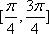
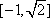
知识点
在△







(1)求角
(2)若

正确答案
(1)
(2)
解析
(1)因为

因为在△




(2)由余弦定理 



因为




知识点
复数
正确答案
解析
知识点
为了参加广州亚运会,从四支较强的排球队中选出18人组成女子排球国家队,队员来源人数如下表:
(1)从这18名队员中随机选出两名,求两人来自同一支队的概率;
(2)中国女排奋力拼搏,战胜韩国队获得冠军,若要求选出两位队员代表发言,设其中来自北京队的人数为


正确答案
见解析。
解析
(1)“从这18名队员中随机选出两名,两人来自于同一队”记作事件A,
则
(2)
∵


∴
∴
知识点
扫码查看完整答案与解析