- 正弦函数的定义域和值域
- 共124题
1
题型:简答题
|
19.如图,几何体














(Ⅰ)求证:
(Ⅱ)求二面角
正确答案
(I)
连接




因为



又面

所以四边形
因为



所以
所以
(II)取




以

则
所以
设面

则

令
设面

则

令
则

解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的定义域和值域
1
题型:填空题
|
13.已知函数


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的定义域和值域三角函数中的恒等变换应用
1
题型:简答题
|
22.设函数f (θ)=sinθ+cosθ,其中,角θ的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点P(x,y),且0≤θ≤π.
(1)若点P的坐标为(
(2)若点P(x,y)为平面区域
正确答案
(1)由点P的坐标和三角函数的定义可得
sinθ=

于是f(θ)=

(2)作出平面区域Ω(即三角区域ABC),
其中A(1,0),B(1,1),C(0,1).
于是0≤θ≤
又f(θ)=

且


故当θ+


f(θ)取得最大值,且最大值等于2 ;
当θ+

f(θ)取得最小值,且最小值等于1.
解析
解析已在路上飞奔,马上就到!
知识点
任意角的三角函数的定义正弦函数的定义域和值域两角和与差的正弦函数
1
题型:
单选题
|
5.已知函数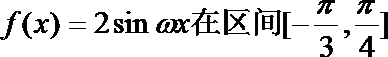
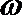
正确答案
D
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的定义域和值域三角函数的最值
1
题型:
单选题
|
8.设随机变量



正确答案
C
解析
解析已在路上飞奔,马上就到!
知识点
正弦函数的定义域和值域
下一知识点 : 正弦函数的单调性
扫码查看完整答案与解析