- 任意角的概念
- 共394题
已知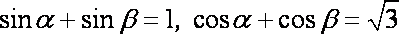
(1)求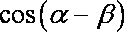
(2)求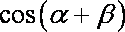
正确答案
见解析。
解析
(1)因为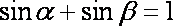
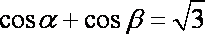
②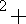
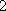
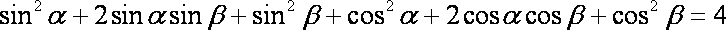
即2+2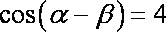
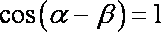
(2)②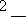
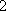
即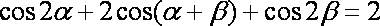
故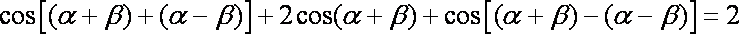
化简得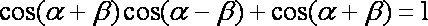
由(1)得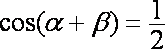
知识点
已知一块半径为r的残缺的半圆形材料ABC,O为半圆的圆心,

正确答案
见解析
解析
如图甲,
设∠DBC=α(
则

所以
=
当且仅当
此时点D到BC的距离为
因此按照图甲方案得到直角三角形的最大面积为
如图乙,
设∠EOD=θ,则OE=rcosθ,DE=rsinθ,
所以

设

当


因为
所以选择图乙的方案,截得的直角三角形面积最大,最大值为
知识点
在△ABC中,已知

正确答案
解析
在△ABC中,已知


∵


则tanC=tan(π﹣A﹣B)=﹣tan(A+B)=


知识点
在



(1)求
(2)若


正确答案
见解析
解析
(1)由正弦定理和

化简,得
即
故
因为sinA≠0,
所以
(2)因为
所以
所以

又因为
整理,得
联立①② 
解得

知识点
已知△ABC的面积为S,角A,B,C的对边分别为a,b,c,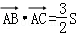
(1)求cosA的值;
(2)若a,b,c成等差数列,求sinC的值。
正确答案
见解析
解析
(1)∵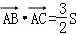
∴ 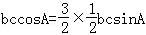
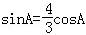
代入sin2A+cos2A=1化简整理,得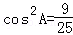
∵ 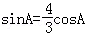
∴角A是锐角,可得
(2)∵ a,b,c成等差数列
∴ 2b=a+c,结合正弦定理得2sinB=sinA+sinC,
即2sin(A+C)=sinA+sinC
因此,可得2sinAcosC+2cosAsinC=sinA+sinC,①
由(1)得
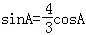

代入①,整理得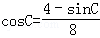
结合sin2C+cos2C=1进行整理,得65sin2C﹣8sinC﹣48=0,
解之得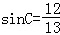

∵ C∈(0,π),可得sinC>0
∴ 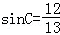
知识点
扫码查看完整答案与解析