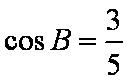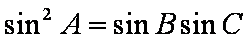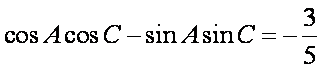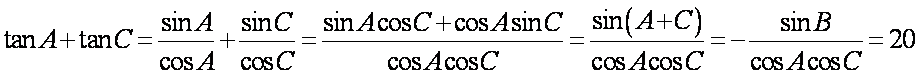- 任意角的概念
- 共394题
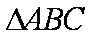
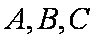
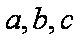

(1)求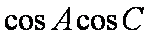
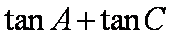
正确答案
见解析
解析
(1)∵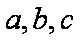
∴
∴由正弦定理得
∵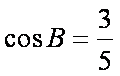
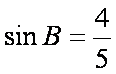
∴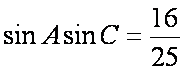
又∵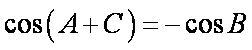
∴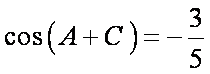
∴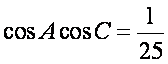
(2)
知识点
在△ABC中,a2+c2=2b2,其中a,b,c分别为角A,B,C所对的边长。
(1)求证:B≤
(2)若
正确答案
见解析。
解析
(1)由余弦定理,得
因


(2)由正弦定理,得
因


因为A为钝角,所以
所以


(2)其它方法:
法1 同标准答案得到


法2 由余弦定理得




法3 由余弦定理得




知识点
如图所示,已知





(1)求
(2)若


正确答案
见解析。
解析
(1)由三角函数的定义知
∴
又由三角函数线知
∵


(2)∵


又


∴
由



知识点
设f(x)=x3,等差数列{an}中a3=7,


(1)求{an}的通项公式和Sn;
(2)求证:Tn<
(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由。
正确答案
见解析。
解析
(1)设数列



解得


∴Sn=

(2) 
∴
(3)由(2)知,

∵
∴ 
当


当


当





当


当


当



所以,此时不存在正整数m,n,且1<m<n,使得
综上,存在正整数m=2,n=16,且1<m<n,使得
知识点
已知
正确答案
解析
解:法1:由已知得
两边平方得

法2:令

所以
知识点
扫码查看完整答案与解析