任意角的概念
共394题

· 任意角的概念

任意角的概念
共394题

热门试卷

X 查看更多试卷

题型：单选题

单选题 · 5 分

已知，且，，则的范围是（）

正确答案

解析

,于是是第三、四象限的角（含轴负半轴）；，于是是第二、三象限的角（含轴正半轴），从而是第三象限的角，选C.

知识点

任意角的概念

题型：简答题

简答题 · 13 分

设三角形的内角的对边分别为，且.

（1）求角的大小；

（2）若，求三角形面积的最大值.

正确答案

见解析。

解析

（1）由正弦定理：可化为

即

所以

又, 所以

因为，所以

（2）由余弦定理得

即

所以，所以

所以三角形面积

知识点

任意角的概念

题型：填空题

填空题 · 5 分

已知O为△ABC的外心，若，则∠C等于　　。

正确答案

解析

解：

设外接圆的半径为R，

∵，

所以，

∴（5+12）2=（13）2，

∴169R2+120=169R2，

∴=0，

∴∠AOB=，

根据圆心角等于同弧所对的圆周的关系如图：

所以△ABC中的内角C值为

故答案为：。

知识点

任意角的概念

题型：简答题

简答题 · 14 分

在△中，已知·=9，sin=cossin，面积S＝6。

（1）求△的三边的长；

（2）设是△（含边界）内一点，到三边，，的距离分别为x，y和z，求x＋y＋z的取值范围。

正确答案

见解析。

解析

设。

（1），，，，

，由，用余弦定理得

（2）

设，由线性规划得。

∴。

知识点

任意角的概念

题型：填空题

填空题 · 5 分

在△ABC中，角A，B，C所对的边分别是a，b，c，若bcosC+ccosB=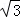acosB，则cosB的值为　　。

正确答案

解析

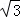
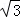
在△ABC中，∵bcosC+ccosB=acosB，由正弦定理定理可得 sinBcosC+cosBsinC=sinAcosB，

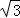
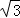
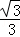
∴sin（B+C）=sinAcosB，即 sinA=sinAcosB，解得 cosB=，

故答案为。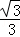

知识点

任意角的概念

继续学习学习下一知识点

下一知识点 : 终边相同的角

百度题库 > 高考 > 文科数学 > 任意角的概念

扫码查看完整答案与解析