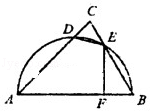- 任意角的概念
- 共394题
如图所示,以直角三角形ABC的直角边AC为直径作⊙O,交斜边AB于点D,过点D作⊙O的切线,交BC边于点E,则
正确答案
解析
连接CD,∵AC是⊙O的直径,∴CD⊥AB。
∵BC经过半径OC的端点C且BC⊥AC,∴BC是⊙O的切线,
而DE是⊙O的切线,∴EC=ED。
∴∠ECD=∠CDE,∴∠B=∠BDE,∴DE=BE。
∴BE=CE=
∴
知识点
如图,在△ABC中,




正确答案
解析
设

则

即







∴


由已知得


∴
故答案为
知识点
在

(1)求
(2)求
正确答案
(1)
解析
(1)解三角形问题,通常利用正余弦定理进行边角转化.由正弦定理得:


得




试题解析:(1)因为
(2)
所以

知识点
在△ABC中,内角A、B、C所对的边分别为a,b,c,已知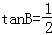
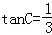
(1)求tanA;
(2)求△ABC的面积。
正确答案
见解析。
解析
(1)因为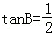
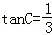
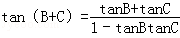
代入得到,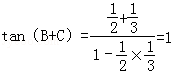
因为A=180°﹣B﹣C,
所以tanA=tan(180°﹣(B+C))
=﹣tan(B+C)=﹣1.
(2)因为0°<A<180°,由(1)结论可得:A=135°,
因为
所以0°<C<B<90°,
所以sinB=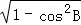
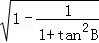
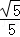
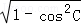
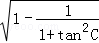

由c=1及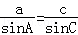
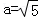
所以△ABC的面积S=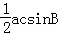
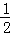
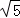
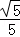
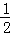
知识点
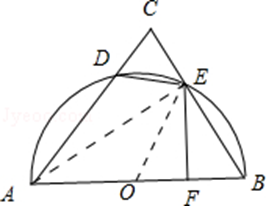
如图,以△ABC的边AB为直径的半圆交AC于点D,交BC于点E,EF⊥AB于点F,AF=3BF,BE=2EC=2.那么CD= 。
正确答案
解析
如图所示,设圆心为点O,半径为R,连接OE,AE。
由AB为⊙O的直径,∴∠AEB=90°,∴AE⊥CE。
∵AF=3FB,AF+FB=2R,
∴FB=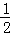
∴∠ABE=60°。
∴AE=BEtan60°=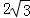
在Rt△ACE,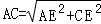
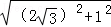
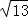
由割线定理可得:CD•CA=CE•CB,∴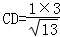
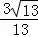
知识点
扫码查看完整答案与解析