- 分层抽样方法
- 共73题
1.一个学校的教师具有高级职称的人数为160,具有中级职称的人数为320,具有初级职称的人数为200,其余人员人数为80。采用分层抽样的方法,从中抽取38人作为职工代表参加教代会。则从上述各层中依次抽取的人数分别是( )
正确答案
解析
教师总人数为160+320+200+80=760,因为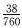
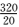
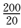
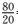
知识点
1.一个学校的教师具有高级职称的人数为160,具有中级职称的人数为320,具有初级职称的人数为200,其余人员人数为80.采用分层抽样的方法,从中抽取38人作为职工代表参加教代会.则从上述各层中依次抽取的人数分别是( )
正确答案
解析
教师总人数为160+320+200+80=760,因为





知识点
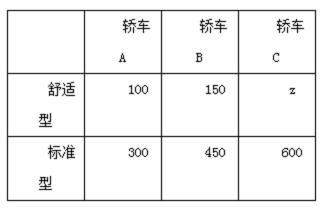
17.一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如右表(单(辆)位: 按类型分层抽样的方法在这个月生产的轿车中抽取50辆, 其中有A类轿车10辆
(1)求z的值;
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率。
正确答案
解: (1)设该厂本月生产轿车为n辆,由题意得,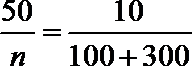
所以n=2000. z=2000-100-300-150-450-600=400
(2)设所抽样本中有m辆舒适型轿车,
因为用分层抽样的方法在C类轿车中抽取一个容量为5的样本,
所以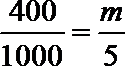
则从中任取2辆的所有基本事件为
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2),
(S2 ,B3),( (S1, S2),(B1 ,B2), (B2 ,B3) ,(B1 ,B3)共10个,
其中至少有1辆舒适型轿车的基本事件有7个基本事件:
(S1, B1), (S1, B2) , (S1, B3) (S2 ,B1), (S2 ,B2), (S2 ,B3),( (S1, S2),
所以从中任取2辆,至少有1辆舒适型轿车的概率为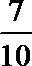
(3)样本的平均数为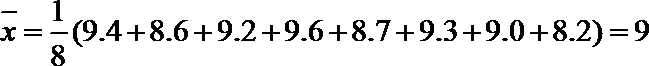
那么与样本平均数之差的绝对值不超过0.5的数为
9.4, 8.6, 9.2, 8.7, 9.3, 9.0这6个数,总的个数为8,
所以该数与样本平均数之差的绝对值不超过0.5的概率为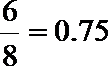
解析
解析已在路上飞奔,马上就到!
知识点
13.给出下列命题: ①线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱; ②由变量x和y的数据得到其回归直线方程L:y =bx + a,则L一定经过点P(x,y);③从匀速传递的产品生产流水线上


正确答案
②④⑤.
解析
①线性相关系数|r|越大,两个变量的线性相关性越强,故①不正确;
②由变量x和y的数据得到其回归直线方程l:y=bx+a,则l一定经过点P故②正确;
③从匀速传递的产品生产流水线上,质检员每10分钟从中抽取一件产品进行某项指标检测,这样的抽样不是分层抽样,故③不正确;
④可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故④正确;
⑤在回归直线方程y=0.1x+10中,当解释变量x每增加一个单位时,预报变量平均增加0.1个单位,故⑤正确.
考查方向
本题线性相关、回归直线方程和拟合等相关概念。
解题思路
认真读题,挨个判断命题的真假
易错点
对上述概念理解的不透彻
知识点
18.为了整顿道路交通秩序,某地考虑将对行人闯红灯进行处罚.为了更好地了解市民的态度,在普通行人中随机选取了200人进行调查,当不处罚时,有80人会闯红灯,处罚时,得到如下数据:
(Ⅰ)当罚金定为10元时,行人闯红灯的概率会比不进行处罚降低多少?
(Ⅱ)将选取的200人中会闯红灯的市民分为两类:A类市民在罚金不超过10元时就会改正行为;B类是其他市民.现对A类与B类市民按分层抽样的方法抽取4人依次进行深度问卷,则前两位均为B类市民的概率是多少?
正确答案
(1)会降低

解析
⑴设“当罚金定为10元时,闯红灯的市民改正行为”为事件

∴当罚金定为10元时,比不制定处罚,行人闯红灯的概率会降低
⑵由题可知































∴抽取4人中前两位均为

考查方向
本题考查了概率统计问题.属于高考中的高频考点
解题思路
1、求出相应的概率
2、利用列举法求解。
易错点
概率表示。
知识点
扫码查看完整答案与解析