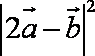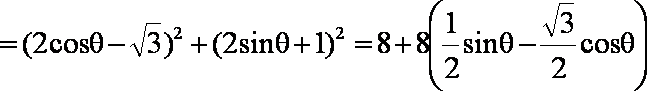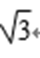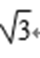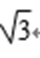- 平面向量的数量积及其应用
- 共555题
已知两个单位向量






正确答案
2
解析
∵


∴tcos60°+1﹣t=0,∴1
知识点
若







正确答案
解析
由题意可得 







解得 cos<


再由<




知识点
已知

(1)求
(2)求函数

正确答案
见解析。
解析
(1)

即

(2)

此时

因此,

知识点
已知向量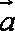
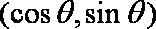
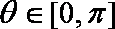
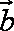
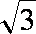
(1)若
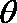
(2)若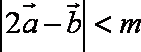
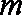
正确答案
见解析。
解析
(1)∵
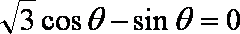
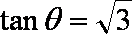
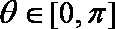
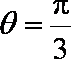
(2)∵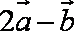
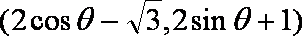
所以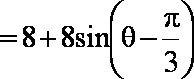
又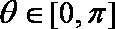
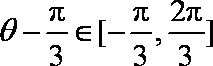
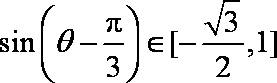
∴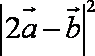
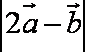
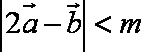

知识点
设函数


轴的交点分别为



正确答案
解析
略
知识点
已知


(1)若
(2)若


正确答案
(1)
解析
(1)



(2)由

由余弦定理可知:
于是ab =4...................10分

知识点
已知向量a=(1,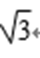
正确答案
解析
略
知识点
已知双曲线


正确答案
解析
由题意可得由题意得A(0,b),C(0,﹣b),B(﹣a,0),F(﹣c,0),
∴







知识点
已知向量





正确答案
解析
由投影的定义可得:



而


知识点
设函数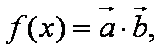
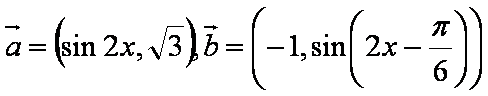
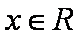
(1)求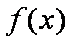
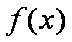
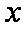
(2)将函数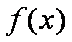
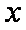
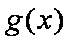
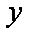
正确答案
见解析。
解析
(1)
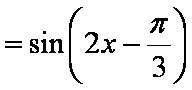
故函数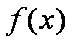
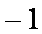
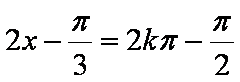
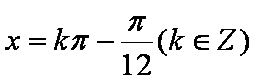
故使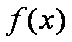
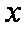
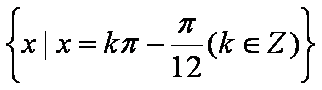
(2)由条件可得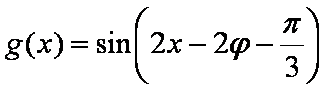
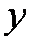
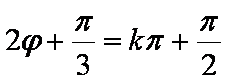
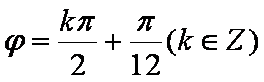
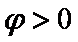
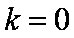
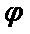
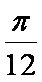
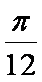
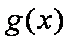
知识点
扫码查看完整答案与解析