- 圆锥曲线的综合问题
- 共478题
如图,已知直线




(1)求

(2)设











(3)在(2)的条件下,记点










正确答案
见解析
解析
(1)由已知,圆


由题设圆心到直线


解得

设




代入直线方程得:
∴

(2)由(1)知抛物线


设



令

所以

∴
∴


(3)设直线
得



则
∴
∵
∴


知识点
如图,已知抛物线










(1)求抛物线
(2)当


(3)若直线



正确答案
(1)

解析
解析:(1)∵点

∴


(2)法一:∵当



设

∴

∴

法二:∵当







联立方程组

∵


同理可得


(3)法一:设


可得,直线

同理,直线

∴

∴直线



∵



法二:设点


以


⊙

①-②得:直线

当



∵



知识点
20.已知椭圆C:+=1(a>b>0)的离心率为,短轴一个端点到右焦点的距离为。
(1)求椭圆C的方程;
(2)设直线l与椭圆C交于A、B两点,坐标原点O到直线l的距离为,求△AOB面积的最大值。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知圆



(1)求椭圆的方程;
(2)过椭圆外一点








正确答案
(1)






(2)设直线



可得:
设

则
化简得:
可得:

解析
解析已在路上飞奔,马上就到!
知识点
20.已知圆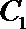
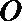
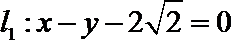
(1)求圆的标准方程;
(2)设点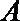
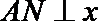

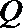
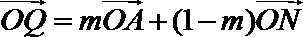
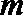
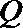

(3)在(2)的结论下,当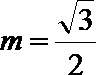
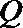
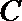
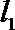
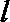

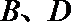
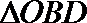
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
14、由直线x=-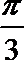
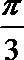
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
11.抛物线


正确答案
解析
解析已在路上飞奔,马上就到!
知识点
19. 已知双曲线



(Ⅰ)如果椭圆

(Ⅱ)如果椭圆




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.已知椭圆C:

(1)求椭圆的方程;
(2)设







正确答案
解析
解析已在路上飞奔,马上就到!
知识点
20.如图,已知抛物线














(1)求圆

(2)若


(3)过直线




正确答案
解析
解析已在路上飞奔,马上就到!
知识点
扫码查看完整答案与解析
































