- 函数模型及其综合应用
- 共70题
18.通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设


(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
正确答案
(1)当





(2)
(3)当



当
当

综上,学生注意力在180以上所持续的时间28.57-4=24.57>24,所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题。
解析
解析已在路上飞奔,马上就到!
知识点
19.某工厂生产某种产品,每日的成本C(单位:元)与日产里



已知每日的利润


(Ⅰ)求
(Ⅱ)当日产量为多少吨时,毎日的利润可以达到最大,并求出最大值。
正确答案
解:(Ⅰ)由题意可得:
解析
解析已在路上飞奔,马上就到!
知识点
20.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元.设该公司一年内生产该品牌服装x千件并全部销售完,每千件的销售收入为
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得的年利润最大。(注:年利润一年销售收入一年总成本)
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
21.已知一家公司生产某种品牌服装的年固定成本为10万元,每生产1千件需另投入2.7万元。设该公司一年内共生产该品牌服装x千件并全部销售完,每千件的销售收入为R(x)万元,且
(1)写出年利润W(万元)关于年产量x(千件)的函数解析式;
(2)年产量为多少千件时,该公司在这一品牌服装的生产中所获得利润最大?
(注:年利润=年销售收入—年总成本)
正确答案
解:(1)当

(2)①当
②当
综合①②知当
解析
解析已在路上飞奔,马上就到!
知识点
21.某商场在国庆促销期间规定:商场内所有商品按标价的80%出售;同时,当顾客在该商场内消费满一定金额后,按如下方案相应获得第二次优惠(获得奖券):
根据上述促销方法,顾客在该商场购物可以获得双重优惠。例如:购买标价为600元的商品,则消费金额为480元,480∈[400,500),所以获得第二次优惠金额为60元,获得的优惠总额为:600×0.2+60=180(元)。
设购买商品的优惠率=
试问:(1)购买一件标价为1000元的商品,顾客得到的优惠率是多少?
(2)设顾客购买标价为x元(x∈[250,1000]) 的商品获得的优惠总额为y元,试建立y关于x的函数关系式;
(3)对于标价在[625,800)(元)内的商品,顾客购买商品的标价的取值范围为多少时,可得到不小于
正确答案
(1)标价为1000元的商品消费金额为800元,获得奖券150元,优惠额为350元,所以优惠率为0.35
(2)y=
(3)购买标价在[625,800)(元)内的商品,消费金额在[500,640)(元)内。
设顾客购买标价为x元的商品,(625≤x<800),消费金额为0.8x.获得奖券100元,此时优惠率为
综上所述,顾客购买标价的取值范围为[625,750](元)时,可得到不小于
解析
解析已在路上飞奔,马上就到!
知识点
17. 某油库的设计容量为30万吨,年初储量为10万吨,从年初起计划每月购进石油 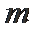
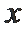
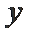
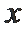

(1)试写出第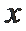
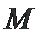
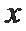
(2)要使16个月内每月按计划购进石油之后,油库总能满足区域内和区域外的需求,且每月石油调出后,油库的石油剩余量不超过油库的容量,试确定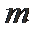
正确答案
见解析
解析
解:(1)
(2)根据题意
所以
即 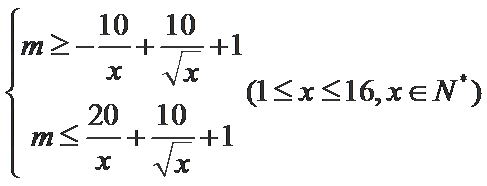
考查方向
解题思路
本题考查函数不等式的应用.解题步骤如下:
(1)求出函数表达式。
(2)根据函数值域,列出不等式。
(3)用换元法求出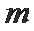
易错点
不等式恒成立分析不够
知识点
某单位有员工1000名,平均每人每年创造利润10万元.为了增加企业竞争力,决定优化产业结构,调整出x (x∈

19.若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
20.在(1)的条件下,若调整出的员工创造出的年总利润始终不高于剩余员工创造的年总利润,则a的取值范围是多少?
正确答案
详见解析
解析
(1)由题意,得10(1000-x)(1+0.2x %)≥10×1000,即
又x>0,所以0<x≤500.即最多调整500名员工从事第三产业. ……5分
考查方向
基本不等式在最值问题中的应用;函数模型的选择与应用.
解题思路
根据题意可列出10(1000-x)(1+0.2x%)≥10×1000,进而解不等式求得x的范围,确定问题的答案
易错点
不能正确的构造出函数的模型,对函数模型掌握不好
正确答案
详见解析
解析
(2)从事第三产业的员工创造的年总利润为
从事原来产业的员工的年总利润为
则

所以ax-

所以ax≤


因为




即x=500时等号成立,所以a≤5,又a>0,所以0<a≤5.
所以a的取值范围为(0,
考查方向
基本不等式在最值问题中的应用;函数模型的选择与应用.
解题思路
根据题意分别表示出从事第三产业的员工创造的年总利润和从事原来产业的员工的年总利润,进而根据题意建立不等式,根据均值不等式求得求a的范围
易错点
不能正确的构造出函数的模型,对函数模型掌握不好
20. 某地区预计明年从年初开始的前x个月内,对某种商品的需求总量

(1)写出明年第x个月的需求量
(2)如果将该商品每月都投放市场p万件,要保持每月都满足市场需求,则p至少为多少万件。
正确答案
解析
解析已在路上飞奔,马上就到!
知识点
8. 已知f(x)=
正确答案
解析
∵ 当x≤1时,f(x)=(4﹣


知识点
扫码查看完整答案与解析