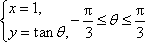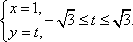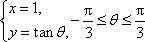- 简单曲线的极坐标方程
- 共19题
在直角坐标系xOy中,圆C1:x2+y2=4,圆C2:(x-2)2+y2=4。
(1)在以O为极点,x轴正半轴为极轴的极坐标系中,分别写出圆C1,C2的极坐标方程,并求出圆C1,C2的交点坐标(用极坐标表示);
(2)求圆C1与C2的公共弦的参数方程。
正确答案
(1) (2,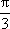
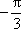
解析
(1)圆C1的极坐标方程为ρ=2,
圆C2的极坐标方程为ρ=4cosθ。
解
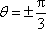
故圆C1与圆C2交点的坐标为(2,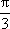
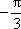
注:极坐标系下点的表示不唯一。
(2)解法一:由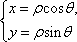
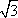
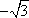
故圆C1与C2的公共弦的参数方程为
(或参数方程写成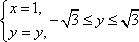
解法二:将x=1代入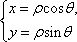
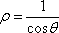
于是圆C1与C2的公共弦的参数方程为
知识点
已知曲线




正确答案
解析
略
知识点
选修4-4:坐标系与参数方程
在直角坐标系xoy中,以坐标原点为极点,x轴为极轴建立极坐标系,半圆C的极坐标方程为

(1)求C的参数方程;
(2)设点D在C上,C在D处的切线与直线
正确答案
(1)C的参数方程
(2)(3/2, 
解析
(1)C的普通方程为 


可得C的参数方程
(2)设D(1+cost,sint).由(Ⅰ)知C是以G(1,0)为圆心,1为半径的上半圆。
因为C在点D处的切线与I垂直,所以直线GD与I的斜率相同。
tant=
故D的直角坐标为(1+cosπ/3,sinπ/3),即(3/2, 
知识点
已知曲线C1的参数方程为
(1)把C1的参数方程化为极坐标方程;
(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π)。
正确答案
(1)ρ2-8ρcos θ-10ρsin θ+16=0.
(2)
解析
(1)将
即C1:x2+y2-8x-10y+16=0.
将
所以C1的极坐标方程为
ρ2-8ρcos θ-10ρsin θ+16=0.
(2)C2的普通方程为x2+y2-2y=0.
由
解得
所以C1与C2交点的极坐标分别为

知识点
在极坐标系中,圆
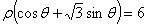
正确答案
1
解析
略
知识点
扫码查看完整答案与解析